题目内容
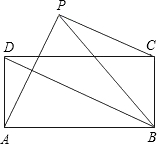 如图,若ABCD是一个长方形,AB=2,AD=1,作点A关于对角线BD的对称点P,则PC等于( )
如图,若ABCD是一个长方形,AB=2,AD=1,作点A关于对角线BD的对称点P,则PC等于( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:连接PD、AC,先根据轴对称的性质得出AD=DP=BC,再由全等三角形的判定定理得到Rt△DPE≌Rt△BCE,从而得到△APC是直角三角形,再利用勾股定理求解即可.
解答: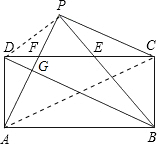 解:连接PD、AC,
解:连接PD、AC,
∵AB与BP关于BD对称,
∴BD是AP的垂直平分线,
∴AD=DP=BC,
∴∠DPB=∠DCB=90°,
在△DPE与△BCE中,
DP=BC,∠DEP=∠BEC,∠DPE=∠DCB=90°,
∴Rt△DPE≌Rt△BCE,
∴PE=CE,DE=EB,
∴∠PCD=∠CDB,
∵∠AFD=∠PFC,∠CDB+∠AFD=90°,
∴∠AFD+∠PCD=90°,
∴∠APC=90°,
在Rt△ABD中,AB=2,AD=1,
∴BD=
=
=
,
∴AC=
,
∵BD是AP的垂直平分线,
∴AG=PG,
∵BD•AG=AD•AB,即
AG=2,AG=
,
∴AP=2AG=
,
在Rt△APC中,
PC=
=
=
.
故选D.
 解:连接PD、AC,
解:连接PD、AC,∵AB与BP关于BD对称,
∴BD是AP的垂直平分线,
∴AD=DP=BC,
∴∠DPB=∠DCB=90°,
在△DPE与△BCE中,
DP=BC,∠DEP=∠BEC,∠DPE=∠DCB=90°,
∴Rt△DPE≌Rt△BCE,
∴PE=CE,DE=EB,
∴∠PCD=∠CDB,
∵∠AFD=∠PFC,∠CDB+∠AFD=90°,
∴∠AFD+∠PCD=90°,
∴∠APC=90°,
在Rt△ABD中,AB=2,AD=1,
∴BD=
| AB2+AD2 |
| 22+12 |
| 5 |
∴AC=
| 5 |
∵BD是AP的垂直平分线,
∴AG=PG,
∵BD•AG=AD•AB,即
| 5 |
2
| ||
| 5 |
∴AP=2AG=
4
| ||
| 5 |
在Rt△APC中,
PC=
| AC2-AP2 |
(
|
3
| ||
| 5 |
故选D.
点评:本题考查的是对称的性质及勾股定理,有一定的难度,能根据题意判断出∠CPF是直角是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
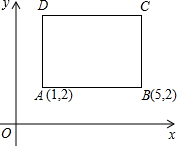 如图,四边形ABCD是一正方形,已知A(1,2),B(5,2)
如图,四边形ABCD是一正方形,已知A(1,2),B(5,2)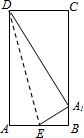 8、如图,四边形ABCD是一张矩形纸片,AD=2AB,若沿过点D的折痕DE将A角翻折,使点A落在BC上的A1处,则∠EA1B=
8、如图,四边形ABCD是一张矩形纸片,AD=2AB,若沿过点D的折痕DE将A角翻折,使点A落在BC上的A1处,则∠EA1B= 8、如图:四边形ABCD是一张矩形纸片,AD=2AB,若沿过点D的折痕DE将A角翻折,使A落在BC上的A1处,则∠EA1B的度数为( )
8、如图:四边形ABCD是一张矩形纸片,AD=2AB,若沿过点D的折痕DE将A角翻折,使A落在BC上的A1处,则∠EA1B的度数为( )
