题目内容
如图，PAB，PCD是⊙O的两条割线，AB是⊙O的直径，AC∥OD．（1）求证：CD=
（2）若
| PA |
| PC |
| 5 |
| 6 |
| AB |
| AD |
分析：（1）由于AC∥OD，OA=OD，故∠1=∠2，∠2=∠3．即∠1=∠3，则
=
，CD=BD；
（2）由于AC∥OD，故
=
，由于
=
，CD=BD，故
=
，因为AB=2AO，所以
=
，又因为AB是⊙O的直径，所以∠ADB=90°，AD2+BD2=AB2，由
=
，设AB=5k，BD=3k，AD=4k，代入代数式即可求解．
 |
| CD |
|
| BD |
（2）由于AC∥OD，故
| PA |
| PC |
| AO |
| CD |
| PA |
| PC |
| 5 |
| 6 |
| AO |
| BD |
| 5 |
| 6 |
| AB |
| BD |
| 5 |
| 3 |
| AB |
| BD |
| 5 |
| 3 |
解答：
解：（1）求证：CD=BD，
证明：∵AC∥OD，
∴∠1=∠2．
∵OA=OD，
∴∠2=∠3．
∴∠1=∠3．
∴
=
．
∴CD=BD．
（2）∵AC∥OD，
∴
=
．
∵
=
，CD=BD，
∴
=
．
∵AB=2AO，
∴
=
．
∵AB是⊙O的直径，
∴∠ADB=90°．
∴AD2+BD2=AB2
∵
=
，设AB=5k，BD=3k，
∴AD=4k．
∴
=
．
解：（1）求证：CD=BD，证明：∵AC∥OD，
∴∠1=∠2．
∵OA=OD，
∴∠2=∠3．
∴∠1=∠3．
∴
|
| CD |
|
| BD |
∴CD=BD．
（2）∵AC∥OD，
∴
| PA |
| PC |
| AO |
| CD |
∵
| PA |
| PC |
| 5 |
| 6 |
∴
| AO |
| BD |
| 5 |
| 6 |
∵AB=2AO，
∴
| AB |
| BD |
| 5 |
| 3 |
∵AB是⊙O的直径，
∴∠ADB=90°．
∴AD2+BD2=AB2
∵
| AB |
| BD |
| 5 |
| 3 |
∴AD=4k．
∴
| AB |
| AD |
| 5 |
| 4 |
点评：本题考查的是平行线的性质及圆周角定理，等腰三角形的，比较复杂，是一道具有综合性的题目．
练习册系列答案
小学同步三练核心密卷系列答案
相关题目
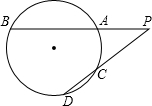如图，PAB、PCD是⊙O的两条割线，PA=3，AB=5，PC=4，则CD等于（ ）| A、6 | ||
| B、2 | ||
C、
| ||
D、
|
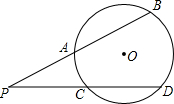如图，PAB、PCD是⊙O的割线，PA=3，PB=6，PC=2，则PD=
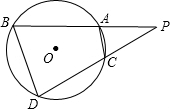如图，PAB、PCD为⊙O的两条割线，若PA=5，AB=7，CD=11，则AC：BD=
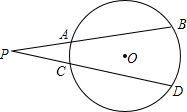如图，PAB和PCD是⊙O的两条割线，弧AC度数为20°，弧BD度数为60°，则∠P=
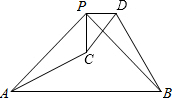（2012•新化县二模）如图，△PAB与△PCD都是等腰直角三角形，∠APB=∠CPD=90°，连接AC、BD，试猜想线段AC和BD的数量关系，并证明你的猜想．