题目内容
4. 如图,已知直线l1:y=-$\frac{3}{4}$x+6与x轴交于点A,与y轴交于点B,将直线l1向下平移4个单位长度后得到直线l2,直线l2与x轴交于点C,与y轴交于点D.
如图,已知直线l1:y=-$\frac{3}{4}$x+6与x轴交于点A,与y轴交于点B,将直线l1向下平移4个单位长度后得到直线l2,直线l2与x轴交于点C,与y轴交于点D.(1)求△AOB的面积;
(2)直线l2的函数表达式是y=-$\frac{3}{4}$x+2.
(3)若点P是折线CAB上一点,且S△PBD=$\frac{1}{2}$S四边形ABCD,请求点P的坐标.
分析 (1)分别令y=-$\frac{3}{4}$x+6中x、y=0求出与之对应的y、x的值,由此即可得出点B、A的坐标,再根据三角形的面积公式即可求出△AOB的面积;
(2)根据直线l1的函数表达式结合“上加下减”的平移规则即可得出直线l2的函数表达式;
(3)根据直线l2的函数表达式利用一次函数图象上点的坐标特征即可求出点C、D的坐标,进而即可求出S四边形ABCD的值,设点P的横坐标为m(0<m≤8),根据三角形的面积公式结合S△PBD=$\frac{1}{2}$S四边形ABCD即可得出关于m的一元一次方程,解之可得出m的值,再根据m的值利用一次函数图象上点的坐标特征即可得出点P的坐标.
解答 解:(1)当x=0时,y=-$\frac{3}{4}$x+6=6,
∴点B的坐标为(0,6);
当y=-$\frac{3}{4}$x+6=0时,x=8,
∴点A的坐标为(8,0).
∴S△AOB=$\frac{1}{2}$OA•OB=$\frac{1}{2}$×8×6=24.
(2)∵将直线l1向下平移4个单位长度后得到直线l2,
∴直线l2的函数表达式是y=-$\frac{3}{4}$x+6-4=-$\frac{3}{4}$x+2.
故答案为:y=-$\frac{3}{4}$x+2.
(3)当x=0时,y=-$\frac{3}{4}$x+2=2,
∴点D的坐标为(0,2);
当y=-$\frac{3}{4}$x+2=0时,x=$\frac{8}{3}$,
∴点C的坐标为($\frac{8}{3}$,0).
∴S四边形ABCD=S△AOB-S△COD=24-$\frac{1}{2}$×2×$\frac{8}{3}$=$\frac{64}{3}$.
设点P的横坐标为m(0<m≤8),
∵S△PBD=$\frac{1}{2}$S四边形ABCD,
∴BD•m=(6-2)m=$\frac{64}{3}$,
解得:m=$\frac{16}{3}$,
∵$\frac{8}{3}$<$\frac{16}{3}$<8,且当x=$\frac{16}{3}$时,y=-$\frac{3}{4}$x+6=-$\frac{3}{4}$×$\frac{16}{3}$+6=2,
∴点P的坐标为($\frac{16}{3}$,0)和($\frac{16}{3}$,2).
点评 本题考查了一次函数图象与几何变换、一次函数图象上点的坐标特征、三角形的面积以及解一元一次方程,熟练掌握图形平移的规律“上加下减,左加右减”是解题的关键.

 如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1)规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换,如此这样,连续经过2017次变换后,正方形ABCD的对角线交点M的坐标变为( )
如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1)规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换,如此这样,连续经过2017次变换后,正方形ABCD的对角线交点M的坐标变为( )| A. | (-2016,2) | B. | (-2016,-2) | C. | (-2015,-2) | D. | (-2015,2) |
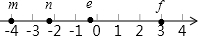 有理数m,n,e,f在数轴上的对应点的位置如图所示,这四个数中,绝对值最小的是( )
有理数m,n,e,f在数轴上的对应点的位置如图所示,这四个数中,绝对值最小的是( )| A. | m | B. | n | C. | e | D. | f |
| A. | x≠2 | B. | x≠-2 | C. | x≠-1 | D. | x=2 |
| A. | ±2 | B. | 2 | C. | -2 | D. | 24 |
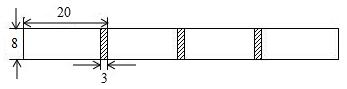
(1)根据题意,将下面的表格补仓完整.
| 白纸张数x(张) | 1 | 2 | 3 | 4 | 5 | … |
| 纸条长度y(cm) | 20 | 37 | 54 | 71 | 88 | … |
(3)要使粘合后的总长度为1006cm,需用多少张这样的白纸?
