题目内容
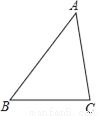
如图,在△ABC中,AB=7,AC=6,∠A=45°,点D、E分别在边AB、BC上,将△BDE沿着DE所在直线翻折,点B落在点P处,PD、PE分别交边AC于点M、N,如果AD=2,PD⊥AB,垂足为点D,那么MN的长是_____.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
如图,在△ABC中,AB=7,AC=6,∠A=45°,点D、E分别在边AB、BC上,将△BDE沿着DE所在直线翻折,点B落在点P处,PD、PE分别交边AC于点M、N,如果AD=2,PD⊥AB,垂足为点D,那么MN的长是_____.

 阅读快车系列答案
阅读快车系列答案