题目内容
6．
如图，在Rt△ABC中，∠A=90°，BC=10，AB=6．（1）用尺规作图的方法作出BC边上的垂直平分线，交AC于点D，交BC于点E．
（2）求AC和AD的长．
分析 （1）直接利用线段垂直平分线的作法进而得出答案；
（2）直接利用勾股定理得出AC的长，再利用线段垂直平分线的性质得出BD=DC，进而求出AD的长．
解答 
解：（1）如图所示：直线DE即为所求；
（2）连接BD，
∵∠A=90°，BC=10，AB=6，
∴AC=$\sqrt{B{C}^{2}-A{B}^{2}}$=8，
∵DE垂直平分线BC，
∴BD=DC，
设AD=x，则DC=BD=8-x，
则x2+62=（8-x）2，
解得：x=$\frac{7}{4}$，
即AD=$\frac{7}{4}$．
点评 此题主要考查了勾股定理以及线段垂直平分线的性质，正确应用勾股定理是解题关键．
练习册系列答案
相关题目
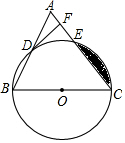如图，已知在△ABC中，BC=AC，以BC为直径的⊙O与边AB、AC分别交于点D，E，DF⊥AC于点F．
如图，点C为直线l上一点，A、B为直线l外两点，过A、B两点分别作直线l的垂线，垂足为点D、E，连接BC、AB，且AB交直线l于点F，若AC=BC，AD=CE，求证：