题目内容
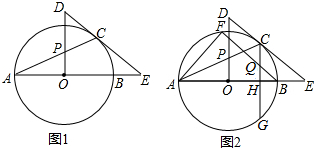
20. 如图,在Rt△ABC中,∠C=90°,∠BAC=60°,将△ABC绕点A逆时针旋转60°后得到△ADE,若AC=1,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是$\frac{π}{2}$(结果保留π).
如图,在Rt△ABC中,∠C=90°,∠BAC=60°,将△ABC绕点A逆时针旋转60°后得到△ADE,若AC=1,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是$\frac{π}{2}$(结果保留π).
分析 根据阴影部分的面积是:S扇形DAB+S△ABC-S△ADE-S扇形ACE,分别求得:扇形BAD的面积、S△ABC以及扇形CAE的面积,即可求解.
解答 解:∵∠C=90°,∠BAC=60°,AC=1,
∴AB=2,
扇形BAD的面积是:$\frac{60×π×{2}^{2}}{360}$=$\frac{2π}{3}$,
在直角△ABC中,BC=AB•sin60°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,AC=1,
∴S△ABC=S△ADE=$\frac{1}{2}$AC•BC=$\frac{1}{2}$×1×$\sqrt{3}$=$\frac{\sqrt{3}}{2}$.
扇形CAE的面积是:$\frac{60π×{1}^{2}}{360}$=$\frac{π}{6}$,
则阴影部分的面积是:S扇形DAB+S△ABC-S△ADE-S扇形ACE
=$\frac{2π}{3}$-$\frac{π}{6}$
=$\frac{π}{2}$.
故答案为:$\frac{π}{2}$.
点评 本题考查了扇形的面积的计算,正确理解阴影部分的面积是:S扇形DAB+S△ABC-S△ADE-S扇形ACE是关键.

练习册系列答案
相关题目
15.用科学记数法表示的数是1.69×105,则原来的数是( )
| A. | 169 | B. | 1690 | C. | 16900 | D. | 169000 |
5.9的绝对值是( )
| A. | 9 | B. | -9 | C. | 3 | D. | ±3 |
12. 如图,把八个等圆按相邻两两外切摆放,其圆心连线构成一个正八边形,设正八边形内侧八个扇形(无阴影部分)面积之和为S1,正八边形外侧八个扇形(阴影部分)面积之和为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )
如图,把八个等圆按相邻两两外切摆放,其圆心连线构成一个正八边形,设正八边形内侧八个扇形(无阴影部分)面积之和为S1,正八边形外侧八个扇形(阴影部分)面积之和为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )
 如图,把八个等圆按相邻两两外切摆放,其圆心连线构成一个正八边形,设正八边形内侧八个扇形(无阴影部分)面积之和为S1,正八边形外侧八个扇形(阴影部分)面积之和为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )
如图,把八个等圆按相邻两两外切摆放,其圆心连线构成一个正八边形,设正八边形内侧八个扇形(无阴影部分)面积之和为S1,正八边形外侧八个扇形(阴影部分)面积之和为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{3}$ | D. | 1 |
9.不等式组$\left\{\begin{array}{l}{x+3>2}\\{1-2x≤-3}\end{array}\right.$的解集是( )
| A. | x≥2 | B. | -1<x≤2 | C. | x≤2 | D. | -1<x≤1 |
14.如果x=-2是方程a(x+1)=2(x-a)的解,则a等于( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{4}$ | C. | -2 | D. | -4 |
 如图,若a∥b,∠1=60°,则∠2的度数为120度.
如图,若a∥b,∠1=60°,则∠2的度数为120度.