题目内容
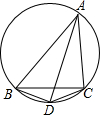 △ABC是⊙O的内接三角形,∠BAC=60°,D是
△ABC是⊙O的内接三角形,∠BAC=60°,D是 | BC |
分析:根据题意求得∠DBC=∠DCB=30°,设BD=DC=x,那么BC=
x,由正弦定理和托勒密定理AB+AC=
a,再根据S四边形ABDC=S△ABD+S△ACD,从而求得答案.
| 3 |
| 3 |
解答:解:解法一:在ABDC中,∠BAC=60度,所以∠BDC=120°,
∵点D是弧BC的中点,
∴BD=DC,
∴∠DBC=∠DCB=30°,
在△BDC中用正弦定理,得
∴BC=
BD,
设BD=DC=x,那么BC=
x,
用托勒密定理:AD•BC=AB•DC+BD•AC,
即
ax=x•AB+x•AC,
则AB+AC=
a,
S四边形ABDC=S△ABD+S△ACD=
(AB•AD•sin∠BAD+AC•AD•sin∠DAC),
=
(AB+AC)AD•sin30°,
=
a2;
解法二:如图,过点D作DE⊥AB,DF⊥AC,垂足分别为E、F,
∵D是
的中点,
∴BD=CD,∠BAD=∠FAD,
∴DE=DF(角平分线上的点到角的两边的距离相等),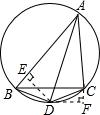
在Rt△DBE与Rt△DCF中,
,
∴Rt△DBE≌Rt△DCF(HL),
∴S△DBE=S△DCF,
∴S四边形ABDC=S四边形AEDF,
∵点D是弧BC的中点,∠BAC=60°,
∴∠BAD=
∠BAC=
×60°=30°,
∵AD=a,
∴AE=AD•cos30°=
a,
DE=AD•sin30•=
a,
∴S四边形AEDF=2S△ADE=2×
×
a×
a=
a2.
故答案为:
a2.
∵点D是弧BC的中点,
∴BD=DC,
∴∠DBC=∠DCB=30°,
在△BDC中用正弦定理,得
∴BC=
| 3 |
设BD=DC=x,那么BC=
| 3 |
用托勒密定理:AD•BC=AB•DC+BD•AC,
即
| 3 |
则AB+AC=
| 3 |
S四边形ABDC=S△ABD+S△ACD=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| ||
| 4 |
解法二:如图,过点D作DE⊥AB,DF⊥AC,垂足分别为E、F,
∵D是
 |
| BC |
∴BD=CD,∠BAD=∠FAD,
∴DE=DF(角平分线上的点到角的两边的距离相等),

在Rt△DBE与Rt△DCF中,
|
∴Rt△DBE≌Rt△DCF(HL),
∴S△DBE=S△DCF,
∴S四边形ABDC=S四边形AEDF,
∵点D是弧BC的中点,∠BAC=60°,
∴∠BAD=
| 1 |
| 2 |
| 1 |
| 2 |
∵AD=a,
∴AE=AD•cos30°=
| ||
| 2 |
DE=AD•sin30•=
| 1 |
| 2 |
∴S四边形AEDF=2S△ADE=2×
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 4 |
故答案为:
| ||
| 4 |
点评:本题考查了圆内接四边形的性质以及圆周角定理,是竞赛题难度偏大.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 如图,⊙O的半径为
如图,⊙O的半径为 如图,△ABC是⊙O的内接三角形,D是
如图,△ABC是⊙O的内接三角形,D是 如图,△ABC是⊙O的内接三角形,∠ACB=75°,∠A=65°,点P在劣弧
如图,△ABC是⊙O的内接三角形,∠ACB=75°,∠A=65°,点P在劣弧 (2012•大连)如图,△ABC是⊙O的内接三角形,若∠BCA=60°,则∠ABO=
(2012•大连)如图,△ABC是⊙O的内接三角形,若∠BCA=60°,则∠ABO=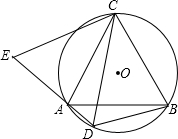 如图,△ABC是⊙O的内接三角形,AC=BC,D为弧AB上一点,延长DA至点E,使CE=CD.若∠ACB=60°
如图,△ABC是⊙O的内接三角形,AC=BC,D为弧AB上一点,延长DA至点E,使CE=CD.若∠ACB=60°