Question

6．如图，AD是△ABC的角平分线，DF⊥AB于点F，DE=DG，△ADG和△AED的面积分别为26和16，则△EDF的面积为5．

Answer 1

分析 过点D作DH⊥AC于H，根据角平分线上的点到角的两边距离相等可得DF=DH，再利用“HL”证明Rt△ADF和Rt△ADH全等，Rt△DEF和Rt△DGH全等，然后根据全等三角形的面积相等列方程求解即可．

解答 解：如图，过点D作DH⊥AC于H，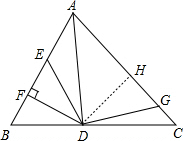

∵AD是△ABC的角平分线，DF⊥AB，
∴DF=DH，
在Rt△ADF和Rt△ADH中，$\left\{\begin{array}{l}{AD=AD}\\{DF=DH}\end{array}\right.$，
∴Rt△ADF≌Rt△ADH（HL），
∴S_Rt△ADF=S_Rt△ADH，
在Rt△DEF和Rt△DGH中，$\left\{\begin{array}{l}{DE=DG}\\{DF=DH}\end{array}\right.$，
∴Rt△DEF≌Rt△DGH（HL），
∴S_Rt△DEF=S_Rt△DGH，
∵△ADG和△AED的面积分别为26和16，
∴16+S_Rt△DEF=26-S_Rt△DGH，
∴S_Rt△DEF=5，
故答案为：5．

点评 本题考查了角平分线上的点到角的两边距离相等的性质，全等三角形的判定与性质，熟记性质并作辅助线构造出全等三角形是解题的关键．