��Ŀ����
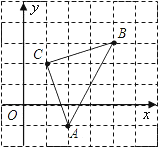
����Ŀ��ij����һ����������״�Ĺ۾�����ABC����������ͼ��ʾ����ͼ�н�����ֱ������ϵ�У������ߵĽ���ʽΪy=��![]() +c�ҹ�����C��0��5�������ȵ�λ��m��
+c�ҹ�����C��0��5�������ȵ�λ��m��
��1��ֱ��д��c��ֵ��
��2�������������ƻ��ع��ŵ�̨�ױ�������һ������Ϊ1.5m�ĵ�̺����̺�ļ۸�Ϊ20Ԫ/m2�������̺�����Ԫ��
��3���ڹ��żӹ�ά��ʱ����ġ����ּܡ�Ϊ����EFGH��H��G�ֱ��������ߵ����Ҳ��ϣ���������б��EG����֪����EFGH���ܳ�Ϊ27.5m����б��EG����б����GEF�Ķ���������ȷ��0.1�㣩

���𰸡�(1)5����2��900Ԫ����3��20.6��.
��������
��1�����ݵ����������������c��
��2�����ݽ���ʽ���A��B��C�������꣬�����̺���ܳ��ȣ��ٸ��ݵ�̺�ļ۸���������̺��Ҫ��Ǯ��
��3������֪����EFGH���ܳ������GF��EF�ߵij��ȣ��ٸ������Ǻ������������б�ǡ�GEF�Ķ�����
��1�������ߵĽ���ʽΪy=��![]() +c��
+c��
�ߵ㣨0��5������������
��c=5��
��2���ɣ�1��֪��OC=5��
��y=0������![]() +5=0�����x1=10��x2=��10��
+5=0�����x1=10��x2=��10��
���̺���ܳ���Ϊ��AB+2OC=20+2��5=30��
��30��1.5��20=900
�𣺹����̺��Ҫ900Ԫ��
��3������G��������m����![]() +5������m��0
+5������m��0
��EF=2m��GF=��![]() +5��
+5��
����֪�ã�2��EF+GF��=27.5��
��2��2m��![]() +5��=27.5��
+5��=27.5��
��ã�m1=5��m2=35���������⣬��ȥ����
��m1=5���룬��![]() +5=��
+5=��![]() ��52+5=3.75��
��52+5=3.75��
���G�������ǣ�5��3.75����
��EF=10��GF=3.75��
��Rt��EFG��tan��GEF=![]() =0.375��
=0.375��
���GEF��20.6�㣮

 ȫ�ܲ����ĩС״Ԫϵ�д�
ȫ�ܲ����ĩС״Ԫϵ�д�