题目内容
16.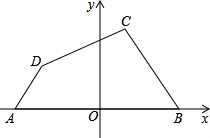 如图A(-4,0),B(6,0),C(2,4),D(-3,2).
如图A(-4,0),B(6,0),C(2,4),D(-3,2).(1)求四边形ABCD的面积;
(2)求△BCD的面积;
(3)在y轴上找一点P,使△APB的面积等于四边形ABCD的一半.求P点坐标.
分析 (1)作DE⊥x轴于E,CF⊥x轴于F,根据梯形的面积公式和三角形面积公式以及四边形ABCD的面积=S△ADE+S四边形CDEF+S△BCF进行计算;
(2)利用四边形ABCD的面积减去三角形ABD的面积即可;
(3)首先求得OP的长,进一步确定P点坐标.
解答 解:(1)如图,
作DE⊥x轴于E,CF⊥x轴于F,
∵A(-4,0),B(6,0),C(2,4),D(-3,2),
∴AE=1,EF=5,BF=4,AB=10,DE=2,CF=4,
∴四边形ABCD的面积=S△ADE+S四边形CDEF+S△BCF
=$\frac{1}{2}$×1×2+$\frac{1}{2}$×(2+4)×5+$\frac{1}{2}$×4×4
=24;
(2)△BCD的面积=四边形ABCD的面积-三角形ABD的面积
=24-$\frac{1}{2}$×10×2
=14;
(3)∵△APB的面积=$\frac{1}{2}$×AB×OP=$\frac{1}{2}$×24,
∴OP=2.4,
∴P点坐标为(0,2.4)或(0,-2.4).
点评 本题考查了坐标与图形性质:利用点的坐标特征计算相应的线段长和判断线段与坐标轴的位置关系;记住各象限内点的坐标特征和坐标上点的坐标特征.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
6.若一次函数y=2x-4上有一点的坐标是(3,2),则方程2x-y-4=0必有一个解为$\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$.
4.下列各式中,正确的是( )
| A. | -(-1)<-(+2) | B. | -$\frac{5}{6}>-\frac{5}{7}$ | C. | -(-5$\frac{1}{2}$)>|-5.5| | D. | -$\frac{7}{8}$$<-\frac{6}{7}$ |
11.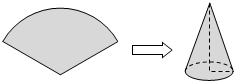 用圆心角为120°,半径为6cm的扇形纸片卷成一个圆锥形无底纸帽(如图所示),则这个纸帽的高是( )
用圆心角为120°,半径为6cm的扇形纸片卷成一个圆锥形无底纸帽(如图所示),则这个纸帽的高是( )
 用圆心角为120°,半径为6cm的扇形纸片卷成一个圆锥形无底纸帽(如图所示),则这个纸帽的高是( )
用圆心角为120°,半径为6cm的扇形纸片卷成一个圆锥形无底纸帽(如图所示),则这个纸帽的高是( )| A. | 4cm | B. | 4$\sqrt{2}$cm | C. | 3$\sqrt{2}$cm | D. | $\sqrt{2}$cm |
1.下列说法正确的是( )
| A. | 某种彩票中奖的概率是1%,因此买100张该彩票一定会中奖 | |
| B. | 一副扑克牌中,随意抽取一张是红桃K,这是必然事件 | |
| C. | 一个袋中装有3个红球、5个白球,任意摸出一个球是红球的概率是$\frac{3}{5}$ | |
| D. | 抛掷两枚普通的硬币,两枚硬币均出现正面向上的概率是25% |
 如图,△ABC中,AB=20,BC=16,AC=13,将△ABC折叠,使一边的两个端点重合,折痕为MN,试求没有重合部分所成的三角形的周长.
如图,△ABC中,AB=20,BC=16,AC=13,将△ABC折叠,使一边的两个端点重合,折痕为MN,试求没有重合部分所成的三角形的周长.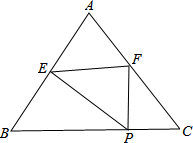 如图,在△ABC中,AB=AC=5,BC=6,点P时边BC上一动点,过点P作PF⊥BC交AC于F,作PE⊥AB于E.
如图,在△ABC中,AB=AC=5,BC=6,点P时边BC上一动点,过点P作PF⊥BC交AC于F,作PE⊥AB于E.