题目内容
11.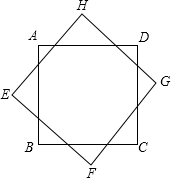 已知,如图,两个全等正方形ABCD,EFGH重叠,重合部分为一个八边形,求八边之间的关系.
已知,如图,两个全等正方形ABCD,EFGH重叠,重合部分为一个八边形,求八边之间的关系.
分析 如图,连结OA、OH,由于正方形ABCD和正方形EFGH全等,则OA=OH,∠OAD=45°,∠OHE=45°,所以∠OAH=∠OHA,则∠PAH=∠PHA,根据等腰三角形的判定得PA=PH,然后利用△HPM、△APQ为等腰直角三角形得到PM=$\sqrt{2}$PH,PQ=$\sqrt{2}$AP,所以PM=PQ,由此可判断八边形的边都相等.
解答 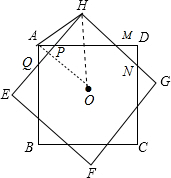 解:点O为两个全等正方形的中心,如图,
解:点O为两个全等正方形的中心,如图,
连结OA、OH,则OA=OH,∠OAD=45°,∠OHE=45°,
∵OA=OH,
∴∠OAH=∠OHA,
∴∠PAH=∠PHA,
∴PA=PH,
∵△HPM、△APQ为等腰直角三角形,
∴PM=$\sqrt{2}$PH,PQ=$\sqrt{2}$AP
∴PM=PQ,
同样可得其它八边形的边相等,
即八边形的边都相等.
点评 本题考查了正方形的性质:正方形的四条边都相等,四个角都是直角;正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;正方形具有四边形、平行四边形、矩形、菱形的一切性质;两条对角线将正方形分成四个全等的等腰直角三角形,同时,正方形又是轴对称图形,有四条对称轴.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
19.若x2-kx+9是完全平方式,则k的值是( )
| A. | ±3 | B. | ±6 | C. | 6 | D. | -6 |
3.下列方程中,没有实数根的是( )
| A. | 5(x2-1)-x=0 | B. | 4(x2+2)=3x | C. | x2-x=100 | D. | -9x2-2x+16=0 |
 用小立方块搭一个几何体,使得它的主视图和左视图如图所示,那么,要摆出这样的几何体最多需要20个小立方块,最少需要6个小方立块.
用小立方块搭一个几何体,使得它的主视图和左视图如图所示,那么,要摆出这样的几何体最多需要20个小立方块,最少需要6个小方立块.