题目内容
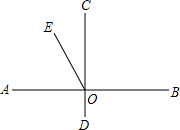如图，AB⊥CD，垂足为O．
（1）比较∠AOD，∠EOB，∠AOE的大小，并用“＜”号连接．
（2）若∠EOC=28°，求∠EOB和∠EOD的度数．
解：∠AOD=90°，∠EOB=90°+∠EOC，∠AOE=90°-∠EOC
∴∠AOE＜∠AOD＜∠EOB
（2）∠EOB=∠EOC+90°=118°
∠AOE=90°-∠EOC=62°
分析：（1）根据图形可判断各角的大小．
（2）∠EOB=∠EOC+90°=118°，∠AOE=90°-∠EOC=62°．
点评：考查角的关系，通过已知角求得未知角．
∴∠AOE＜∠AOD＜∠EOB
（2）∠EOB=∠EOC+90°=118°
∠AOE=90°-∠EOC=62°
分析：（1）根据图形可判断各角的大小．
（2）∠EOB=∠EOC+90°=118°，∠AOE=90°-∠EOC=62°．
点评：考查角的关系，通过已知角求得未知角．
练习册系列答案
相关题目
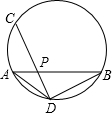
如图，AB为⊙O的直径，C为⊙O上一点，AD和过C点的切线互相垂直，垂足为D．
如图，AB为⊙O的直径，C为⊙O上一点，AD和过C点的切线互相垂直，垂足为D，锐角∠DAB的平分线AC交⊙O于点C，作CD⊥AD，垂足为D，直线CD与AB的延长线交于点E．
（2013•保定一模）如图，AB表示的是某单位办公楼的高，AE表示从楼顶垂挂下的宣传条幅，其长为30米，CD表示张明同学所处的位置与高度，张明同学测得条幅顶端A的仰角为60°，测得条幅底端E的仰角为30°．求张明同学到办公楼的水平距离（精确到整米数）．
，求垂线段OE的长．