题目内容
如图,数轴上有三个点A、B、C,表示的数分别是﹣4、﹣2、3,请回答:
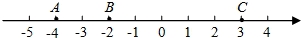
(1)若使C、B两点的距离与A、B两点的距离相等,则需将点C向左移动__________个单位;
(2)若移动A、B、C三点中的两个点,使三个点表示的数相同,移动方法有__________种,其中移动所走的距离和最小的是__________个单位;
(3)若在原点处有一只小青蛙,一步跳1个单位长.小青蛙第1次先向左跳1步,第2次再向右跳3步,然后第3次再向左跳5步,第4次再向右跳7步,…,按此规律继续跳下去,那么跳第100次时,应跳__________步,落脚点表示的数是__________;
(4)数轴上有个动点表示的数是x,则|x﹣2|+|x+3|的最小值是__________.
【考点】数轴;绝对值.
【分析】(1)由AB=2,结合数轴即可得出点C向左移动的距离;
(2)分为三种:移动B、C;移动A、C;移动A、B.然后计算每种情况移动所走的距离和即可;
(3)根据规律发现,所跳步数是奇数列,写出表达式,然后把n=100代入进行计算即可求解,根据向左跳是负数,向右跳是正数,列出算式,然后两个数一组,计算后再求和即可,当跳了n次时,分n是偶数与n是奇数两种情况讨论求解.
(4)根据绝对值的意义,可知|x﹣2|是数轴上表示数x的点与表示数2的点之间的距离,|x+3|是数轴上表示数x的点与表示数﹣3的点之间的距离,现在要求|x﹣2|+|x+3|的最小值,由线段的性质,两点之间,线段最短,可知当﹣3≤x≤2时,|x﹣2|+|x+3|有最小值.
【解答】解:(1)有数轴可知:A、B两点的距离为2,B点、C点表示的数分别为:﹣2、3,
所以当C、B两点的距离与A、B两点的距离相等时,需将点C向左移动3个单位,故答案为:3;
(2)有3种方法:①移动B、C,把点B向左移动2个单位长度,把C向左移动7个单位长度,移动距离之和为:2+7=9;
②移动A、C,把点A向右移动2个单位长度,把C向左移动5个单位长度,移动距离之和为:2+5=7;
③移动B、A,把点A向右移动7个单位长度,把B向左右移动5个单位长度,移动距离之和为:7+5=12.
所以移动所走的距离和最小的是7个单位,
故答案为:3,7;
(3)∵第1次跳1步,第2次跳3步,第3次跳5步,第4次跳7步,
…
∴第n次跳(2n﹣1)步,
当n=100时,2×100﹣1=200﹣1=199,
此时,所表示的数是:﹣1 +3﹣5+7﹣…﹣197+199,
+3﹣5+7﹣…﹣197+199,
=(﹣1+3)+(﹣5+7)+…+(﹣197+199),
=2×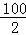
=100,
(4)根据题意,可知当﹣3≤x≤2时,|x﹣2|+|x+3|有最小值.
此时|x﹣2|=2﹣x,|x+3|=x+3,
∴|x﹣2|+|x+1|=2﹣x+x+3=5.
∴则|x﹣2|+|x+3|的最小值是5.
故答案为 :(1)3;(3)3,7;(4)199,100;(5)5.
:(1)3;(3)3,7;(4)199,100;(5)5.
【点评】本题借助数轴考查了数轴上两点之间的距离的求解问题,以及数字变化规律的探讨问题,综合性较强,难度较大,但只要仔细分析,从中理清问题变化的思路便不难求解,此题计算求解时一定要仔细认真.

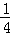 (﹣4a2+2a﹣8b)﹣(﹣a﹣2b),其中a=
(﹣4a2+2a﹣8b)﹣(﹣a﹣2b),其中a=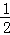 ,b=2015.
,b=2015. 人 D.
人 D.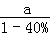 人
人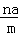 表示的实际意义是__________.
表示的实际意义是__________. =32;3×5+1=16=42;4×6+1=25=52,…
=32;3×5+1=16=42;4×6+1=25=52,…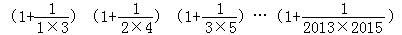 .
.