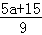题目内容
观察算式:1×3+1=4=22;2×4+1=9 =32;3×5+1=16=42;4×6+1=25=52,…
=32;3×5+1=16=42;4×6+1=25=52,…
(1)请根据你发现的规律填空:6×8+1=__________;
(2)用含n的等式表示上面的规律:__________;
(3)用找到的规律解决下面的问题:
计算: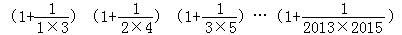 .
.
【考 点】规律型:数字的变化类.
点】规律型:数字的变化类.
【分析】(1)(2)等式的左边是相差为2的两个数相乘,再加上1;右边是两个数的平均数的平方,由此规律得出答案即可;
(3)利用以上规律,计算交错约分得出答案即可.
【解答】解:(1)∵1×3+1=4=22
2×4+1=9=32
3×5+1=16=42
4×6+1=25=52
…
∴6×8+1=72;
(2)由(1)可得出,第n个式子表达式为:n(n+2)+1=(n+1)2;
(3)原式=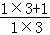 ×
×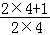 ×
×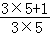 ×…×
×…×
=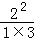 ×
×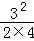 ×
×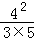 ×…×
×…×
=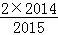
=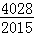 .
.
【点评】此题主要考查了数字变化规律,根据已知得出数字中的变与不变是解题关键.

练习册系列答案
相关题目
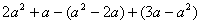
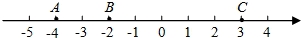
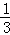 ,+10,20%,
,+10,20%,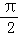 ,0,﹣0.2020020002…(每两个2之间依次增加1个0),0.333….
,0,﹣0.2020020002…(每两个2之间依次增加1个0),0.333….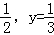 .
. 学生a人,其中女生人数比男生人数的
学生a人,其中女生人数比男生人数的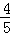 多3人,则女生的人数为( )
多3人,则女生的人数为( ) B.
B.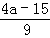 C.
C.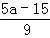 D.
D.