题目内容
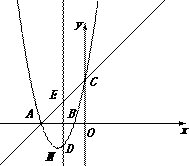
如图,抛物线经过A( ),B(
),B( ),C(
),C( )三点.
)三点.
(1)求抛物线的解析式;
(2)在直线AC下方的抛物线上有一点D,使得△DCA的面积最大,求点D的坐标;
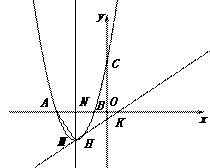
(3)设点M是抛物线的顶点,试判断抛物线上是否存在点H满足 ?若存在,请求出点H的坐标;若不存在,请说明理由.
?若存在,请求出点H的坐标;若不存在,请说明理由.
 |
解:(1)∵该抛物线过点C(0,2),
∴可设该抛物线的解析式为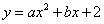 .
.
将A(-2,0),B(-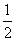 ,0)代入,得
,0)代入,得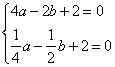 ,
,
解得: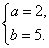
∴此抛物线的解析式为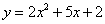 ;……………………………………………4分
;……………………………………………4分
(2)由题意可求得直线AC的解析式为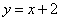 .………………………………………5分
.………………………………………5分
 如图,设D点的横坐标为t(-2<t<0),则D点的纵坐标为
如图,设D点的横坐标为t(-2<t<0),则D点的纵坐标为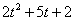 .
.
过D作y轴的平行线交AC于E.
∴E点的坐标为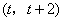 .
.
∴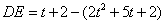
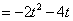 ,用h表示点C到线段DE所在直线的距离,
,用h表示点C到线段DE所在直线的距离,
∴
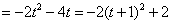 ………………………………………………7分
………………………………………………7分
∵-2<t<0
∴当t=-1时,△DAC面积最大,此时点D的坐标为(-1,-1).…………………8分
(3)点H存在.………………………………………………………………………9分
由(1)知,点M的坐标为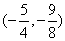
解法一:如图,假设存在点H,满足
作直线MH交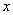 轴于点K(
轴于点K(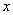 ,0),作MN⊥
,0),作MN⊥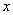 轴于点N.
轴于点N.
 ∵
∵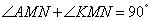 ,
,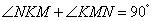
∴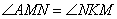
∵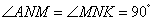
∴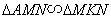
∴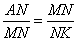
∴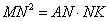
∴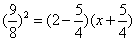
∴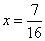
∴点K的坐标为(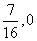 )……………………………………………………………11分
)……………………………………………………………11分
所以直线MK的解析式为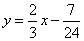 .
.
∴ 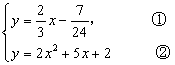 把①代入②,化简,得:
把①代入②,化简,得: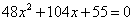 .
.
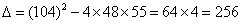 >0. …………………………………12分
>0. …………………………………12分
∴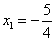 ,
,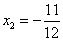 .将
.将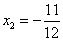 代入
代入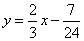 中,解得
中,解得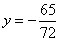
∴ 直线MN与抛物线有两个交点(其中一点为顶点M).
∴ 抛物线上必存在一点H,使∠AMH=90?,
此时点H坐标为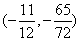 .…………………………………………………13分
.…………………………………………………13分
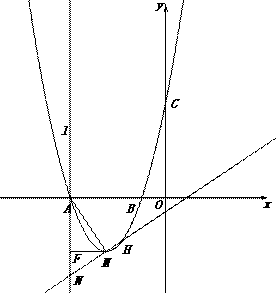
解法二: 如图,过点A作直线
如图,过点A作直线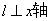 ,过顶点M作MN⊥AM,MF
,过顶点M作MN⊥AM,MF 分别交直线
分别交直线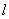 于点N和点F.则 ∠FMN+∠AMF=90?.
于点N和点F.则 ∠FMN+∠AMF=90?.
∵ ∠MAF+∠AMF=90?,
∴ ∠MAF=∠FMN.
又∵ ∠AFM=∠MFN=90?,
∴ △AFM∽△MFN.
 ∴ AF∶MF=MF∶FN. 即
∴ AF∶MF=MF∶FN. 即 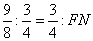
∴ FN=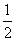 .
.
∴ 点N的坐标为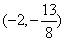 . …………………11分
. …………………11分
设过点M,N的直线的解析式为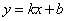 .
.
将M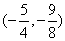 ,N
,N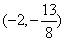 代入得:
代入得:
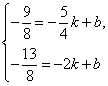 解得:
解得: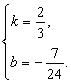
所以直线MN的解析式为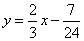
∴ 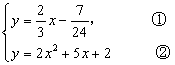 把①代入②,化简,得:
把①代入②,化简,得: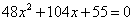 .
.
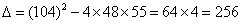 >0.…………………………………12分
>0.…………………………………12分
∴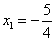 ,
,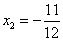 .将
.将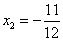 代入
代入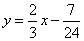 中,解得
中,解得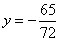
∴ 直线MN与抛物线有两个交点(其中一点为顶点M).
∴ 抛物线上必存在一点H,使∠AMH=90?,
此时点H坐标为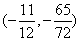 .
.

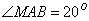 ,N是弧MB的中点,P是直径AB上的一动点,若MN=1,则
,N是弧MB的中点,P是直径AB上的一动点,若MN=1,则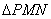 周长的最小值为( )
周长的最小值为( )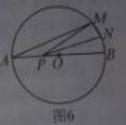
 ,B处的俯角为
,B处的俯角为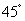 .如果此时直升机镜头C处的高度CD为200米,点A、D、B在同一直线上,则AB两点的距离是
.如果此时直升机镜头C处的高度CD为200米,点A、D、B在同一直线上,则AB两点的距离是 
 卷调查,学生可根据自己的喜好选修一门,李老师对某班全班同学的选课情况进行统计后,制成了两幅不完整的统计图(如图).
卷调查,学生可根据自己的喜好选修一门,李老师对某班全班同学的选课情况进行统计后,制成了两幅不完整的统计图(如图).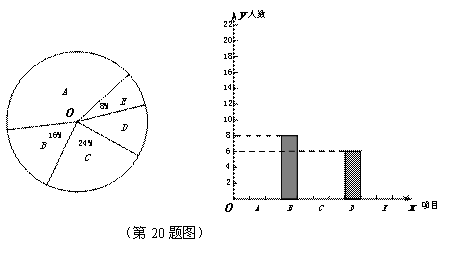







 ) (D)
) (D) 
 的结果是
的结果是 B、
B、 C、
C、 D、
D、
