题目内容
梯形同一底上的两个角分别为70°和55°，且梯形的上底为7cm，下底为12cm，则与70°角相邻的腰长为
5
5
cm．分析：根据已知画出图形，进而利用等腰三角形的性质得出BC=EC，ED=AD，即可得出答案．
解答：
解：如图所示：延长BA、DC交于点E，
∵梯形同一底上的两个角分别为70°和55°，梯形的上底为7cm，下底为12cm
则∠B=55°，∠C=70°，
∴∠E=180°-∠B-∠C=55°，
∴BC=EC=12cm，
∵AD∥BC，
∴∠EAD=∠B，
∴∠E=∠EAD，
∴ED=AD=7cm，
∴CD=EC-ED=12-7=5（cm），
∴与70°角相邻的腰长为5cm．
故答案为：5．
解：如图所示：延长BA、DC交于点E，∵梯形同一底上的两个角分别为70°和55°，梯形的上底为7cm，下底为12cm
则∠B=55°，∠C=70°，
∴∠E=180°-∠B-∠C=55°，
∴BC=EC=12cm，
∵AD∥BC，
∴∠EAD=∠B，
∴∠E=∠EAD，
∴ED=AD=7cm，
∴CD=EC-ED=12-7=5（cm），
∴与70°角相邻的腰长为5cm．
故答案为：5．
点评：此题主要考查了梯形的性质以及等腰三角形的性质，根据题意得出AD=ED，BC=EC是解题关键．
练习册系列答案
相关题目
下列各命题正确的是（ ）
A、
| ||||
| B、梯形同一底上的两个角相等 | ||||
| C、过一点有且只有一条直线与已知直线平行 | ||||
| D、两条直线被第三条直线所截，同位角相等 |
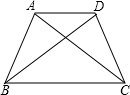如图，四边形ABCD是等腰梯形，AD∥BC，AB=CD，则AC=