题目内容
我们规定:形如 的函数叫做“奇特函数”.当
的函数叫做“奇特函数”.当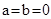 时,“奇特函数”
时,“奇特函数”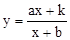 就是反比例函数
就是反比例函数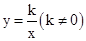 .
.
(1) 若矩形的两边长分别是2和3,当这两边长分别增加x和y后,得到的新矩形的面积为8 ,求y与x之间的函数关系式,并判断这个函数是否为“奇特函数”;
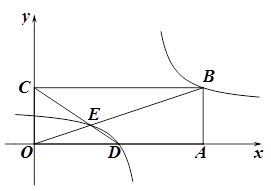
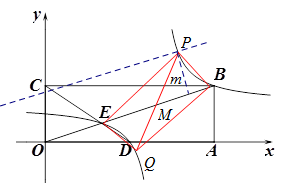
(2) 如图,在平面直角坐标系中,点O为原点,矩形OABC的顶点A,C的坐标分别为(9,0)、(0,3).点D是OA的中点,连结OB,CD交于点E,“奇特函数”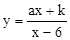 的图象经过B,E两点.
的图象经过B,E两点.
① 求这个“奇特函数”的解析式;
② 把反比例函数 的图象向右平移6个单位,再向上平移 个单位就可得到①中所得“奇特函数”的图象.过线段BE中点M的一条直线l与这个“奇特函数”的图象交于P,Q两点,若以B、E、P、Q为顶点组成的四边形面积为
的图象向右平移6个单位,再向上平移 个单位就可得到①中所得“奇特函数”的图象.过线段BE中点M的一条直线l与这个“奇特函数”的图象交于P,Q两点,若以B、E、P、Q为顶点组成的四边形面积为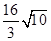 ,请直接写出点P的坐标.
,请直接写出点P的坐标.
 的函数叫做“奇特函数”.当
的函数叫做“奇特函数”.当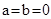 时,“奇特函数”
时,“奇特函数”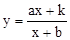 就是反比例函数
就是反比例函数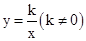 .
.(1) 若矩形的两边长分别是2和3,当这两边长分别增加x和y后,得到的新矩形的面积为8 ,求y与x之间的函数关系式,并判断这个函数是否为“奇特函数”;
(2) 如图,在平面直角坐标系中,点O为原点,矩形OABC的顶点A,C的坐标分别为(9,0)、(0,3).点D是OA的中点,连结OB,CD交于点E,“奇特函数”
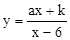 的图象经过B,E两点.
的图象经过B,E两点.① 求这个“奇特函数”的解析式;
② 把反比例函数
 的图象向右平移6个单位,再向上平移 个单位就可得到①中所得“奇特函数”的图象.过线段BE中点M的一条直线l与这个“奇特函数”的图象交于P,Q两点,若以B、E、P、Q为顶点组成的四边形面积为
的图象向右平移6个单位,再向上平移 个单位就可得到①中所得“奇特函数”的图象.过线段BE中点M的一条直线l与这个“奇特函数”的图象交于P,Q两点,若以B、E、P、Q为顶点组成的四边形面积为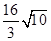 ,请直接写出点P的坐标.
,请直接写出点P的坐标.
(1)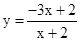 ,是 “奇特函数”;(2)①
,是 “奇特函数”;(2)①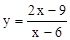 ;②
;②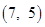 或
或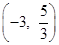 或
或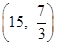 或
或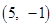 .
.
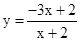 ,是 “奇特函数”;(2)①
,是 “奇特函数”;(2)①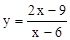 ;②
;②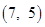 或
或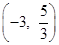 或
或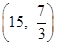 或
或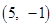 .
.试题分析:(1)根据题意列式并化为
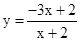 ,根据定义作出判断.
,根据定义作出判断.(2)①求出点B,D的坐标,应用待定系数法求出直线OB解析式和直线CD解析式,二者联立即可得点E 的坐标,将B(9,3),E(3,1)代入函数
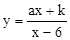 即可求得这个“奇特函数”的解析式.
即可求得这个“奇特函数”的解析式.②根据题意可知,以B、E、P、Q为顶点组成的四边形是平行四边形BPEQ或BQEP,据此求出点P的坐标.
试题解析:(1)根据题意,得
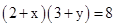 ,
,∵
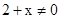 ,∴
,∴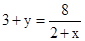 .∴
.∴ .
.根据定义,
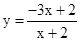 是 “奇特函数”.
是 “奇特函数”.(2)①由题意得,
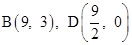 .
.易得直线OB解析式为
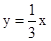 ,直线CD解析式为
,直线CD解析式为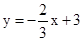 ,
,由
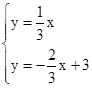 解得
解得 .∴点E(3,1).
.∴点E(3,1).将B(9,3),E(3,1)代入函数
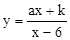 ,得
,得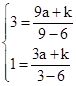 ,整理得
,整理得 ,解得
,解得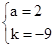 .
.∴这个“奇特函数”的解析式为
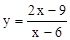 .
.②∵
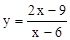 可化为
可化为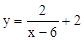 ,
,∴根据平移的性质,把反比例函数
 的图象向右平移6个单位,再向上平移2个单位就可得到
的图象向右平移6个单位,再向上平移2个单位就可得到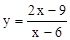 .
.∴
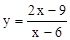 关于点(6,2)对称.
关于点(6,2)对称.∵B(9,3),E(3,1),∴BE中点M(6,2),即点M是
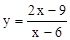 的对称中心.
的对称中心.∴以B、E、P、Q为顶点组成的四边形是平行四边形BPEQ或BQEP.
由勾股定理得,
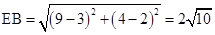 .
.设点P到EB的距离为m,
∵以B、E、P、Q为顶点组成的四边形面积为
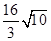 ,
,∴
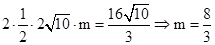 .
.∴点P在平行于EB的直线
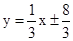 上.
上.∵点P在
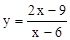 上,
上,∴
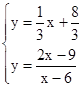 或
或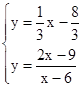 .
.解得
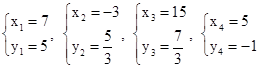 .
.∴点P的坐标为
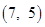 或
或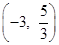 或
或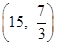 或
或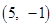 .
.

练习册系列答案
相关题目
 (x>0)图象上.
(x>0)图象上.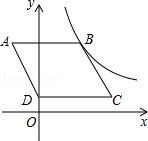
 的坐标为(
的坐标为( ,
,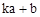 )(其中k为常数,且
)(其中k为常数,且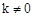 ),则称点
),则称点 ,
,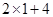 ),即
),即 的“2属派生点”
的“2属派生点”  为等腰直角三角形,则k的值为____________;
为等腰直角三角形,则k的值为____________;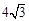 ),点A在函数
),点A在函数 的图象上,且点A是点B的“
的图象上,且点A是点B的“ 属派生点”,当线段B Q最短时,求B点坐标.
属派生点”,当线段B Q最短时,求B点坐标.
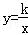 (x>0)的图象经过矩形OABC对角线的交点M,分别于AB、BC交于点D、E,若四边形ODBE的面积为9,则k的值为( )
(x>0)的图象经过矩形OABC对角线的交点M,分别于AB、BC交于点D、E,若四边形ODBE的面积为9,则k的值为( )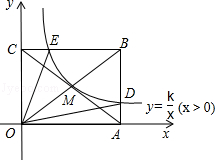


 .
.
 的图象上一点,AB⊥y轴于B,且△ABO的面积为3,则k的值为 .
的图象上一点,AB⊥y轴于B,且△ABO的面积为3,则k的值为 .
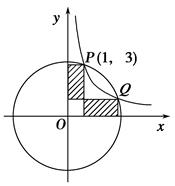
 (k>0)与⊙O在第一象限内交于P、Q 两点,分别过P、Q两点向x轴和y轴作垂线,已知点P坐标为(1,3),则图中阴影部分的面积为________.
(k>0)与⊙O在第一象限内交于P、Q 两点,分别过P、Q两点向x轴和y轴作垂线,已知点P坐标为(1,3),则图中阴影部分的面积为________.