题目内容
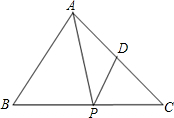如图，已知△ABC的面积是12，BC=6．P点在BC边上滑动，PD∥AB交AC于D．如果BP=x，△APD的面积为y，求y与x的函数关系，并求出函数的定义域．考点：相似三角形的判定与性质
专题：计算题
分析：由PD∥AB，根据相似三角形的判定得到△CPD∽△CBA，再根据相似的性质得
=（
）2=（
）2，所以S△CPD=
（6-x）2；由PD∥AB，根据平行线分线段成比例的性质得
=
=
，然后根据三角形面积公式得
=
，所以S△APD=
（6-x）2•
，再化简即可．
| S△CPD |
| S△CBA |
| CP |
| CB |
| 6-x |
| 6 |
| 1 |
| 3 |
| AD |
| DC |
| BP |
| PC |
| x |
| 6-x |
| S△APD |
| S△CPD |
| AD |
| DC |
| 1 |
| 3 |
| x |
| 6-x |
解答：解：∵BC=6，BP=x，
∴PC=6-x
∵PD∥AB，
∴△CPD∽△CBA，
∴
=（
）2=（
）2，
∴S△CPD=12×
=
（6-x）2，
∵PD∥AB，
∴
=
=
，
∵
=
，
∴S△APD=
（6-x）2•
=-
x2+2x（0＜x＜0）．
∴PC=6-x
∵PD∥AB，
∴△CPD∽△CBA，
∴
| S△CPD |
| S△CBA |
| CP |
| CB |
| 6-x |
| 6 |
∴S△CPD=12×
| (6-x)2 |
| 36 |
| 1 |
| 3 |
∵PD∥AB，
∴
| AD |
| DC |
| BP |
| PC |
| x |
| 6-x |
∵
| S△APD |
| S△CPD |
| AD |
| DC |
∴S△APD=
| 1 |
| 3 |
| x |
| 6-x |
| 1 |
| 3 |
点评：本题考查了相似三角形的判定与性质：平行于三角形一边的直线与其他两边所截的三角形与原三角形相似；相似三角形对应边的比相等，都等于相似比；相似三角形面积的比等于相似比的平方．也考查了三角形的面积公式．
练习册系列答案
相关题目
不等式组解集如图所示，则其解集为（ ）| A、0≤x＜1 | B、x＜1 |
| C、x≤0 | D、0＜x＜1 |
两个连续奇数中，较小的是2n-1，那么较大的奇数是（ ）
| A、2n | B、n+1 |
| C、2n+1 | D、2n+2 |
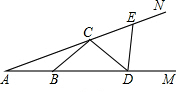如图，点B，D在射线AM上，点C，E在射线AN上，且AB=BC=CD=DE，已知∠EDM=84°，求∠A的度数．