Question

【题目】在平面直角坐标系中，Rt△AOB的两条直角边OA、OB分别在x轴和y轴上，OA=3，OB=4．把△AOB绕点A顺时针旋转120°，得到△ADC．边OB上的一点M旋转后的对应点为M′，当AM′+DM取得最小值时，点M的坐标为（　　）

A. （0， ） B. （0，） C. （0，） D. （0，3）

Answer 1

【答案】A

【解析】

根据旋转的性质得到AM＝AM′，得出AM′＋DM的最小值＝AM＋DM的最小值，作点D关于直线OB的对称点D′，连接AD′交OB于M，则AD′＝AM′＋DM的最小值，过D作DE⊥x轴于E，解直角三角形得到DE＝×3＝，AE＝，求出D（，），根据轴对称的性质得到D′（，），求出直线AD′的解析式为y＝x＋，于是得到结论．

∵把△AOB绕点A顺时针旋转120°，得到△ADC，点M是BO边上的一点，

∴AM＝AM′，

∴AM′＋DM的最小值＝AM＋DM的最小值，

作点D关于直线OB的对称点D′，连接AD′交OB于M，

则AD′＝AM′＋DM的最小值，

过D作DE⊥x轴于E，

∵∠OAD＝120°，

∴∠DAE＝60°，

∵AD＝AO＝3，

∴DE＝×3＝，AE＝，

∴D（，），

∴D′（ ，），

设直线AD′的解析式为y＝kx＋b，

∴，

∴

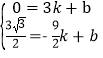∴直线AD′的解析式为y＝x＋，

当x＝0时，y＝，

∴M（0，），

故选：A．