Question

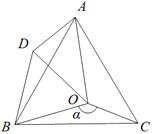
【题目】如图，P是等边三角形ABC内一点，且PA=4，PB=，PC=2，以下五个结论：①∠ BPC=120°；②∠APC=120°；③；④AB=；⑤点P到△ABC三边的距离分别为PE,PF,PG,则有 其中正确的有（ ）

A.4个B.3个C.2个D.1个

Answer 1

【答案】B

【解析】

作BH⊥PC于H，根据等边三角形的性质得：BA=BC，∠ABC=60°，把△ABP绕点B顺时针旋转60°得到△CBD，证明出△PBD为等边三角形和△PCD为直角三角形即可求出①；根据平角性质，可得∠BPH=30°，证明△ABP为直角三角形，即可求出②和④；根据面积公式求出③；根据等面积法即可求出④.

作BH⊥PC于H

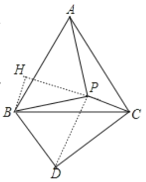
根据等边三角形的性质得：BA=BC，∠ABC=60°

把△ABP绕点B顺时针旋转60°得到△CBD，连接PD得到上图

根据旋转的性质可得CD=AP=4，BD=BP=，∠PBD=60°

∴△PBD为等边三角形

∴PD=PB=，∠BPD=60°

在三角形PDC中，PC=2，PD= ，CD=4

∴PC2+PD2=CD2

∴△PCD为直角三角形，∠CPD=90°

∴∠BPC=∠BPD+∠CPB=150°，故①错误；

根据平角性质，可得∠BPH=30°

在直角三角形PBH中，∵∠BPH=30°

∴PB=

∴BH=，则PH=3

CH=PC+PH=2+3=5

在直角三角形BCH中

，则，故④正确；

又∵

∴△ABP为直角三角形，∠APB=90°

∴∠APC=360°-∠APB-∠BPC=120°，故选项②正确；

，故选项③错误；

∴，故选项⑤正确

故答案选择：B.