题目内容
14.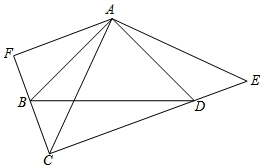 如图,∠BAD=∠CAE=90°,AB=AD,AC=AE,AF⊥CF,垂足为F.
如图,∠BAD=∠CAE=90°,AB=AD,AC=AE,AF⊥CF,垂足为F.(1)求证:△ABC≌△ADE;
(2)求证:CA平分∠ECF;
(3)请指出CE与AF有怎样的数量关系,并说明理由.
分析 (1)根据两边夹角对应相等的两个三角形全等,即可证明.
(2)想办法证明∠ACB=∠ACE=45°即可解决问题.
(3)结论:CE=2AF.过点A作AG⊥CG,垂足为点G.先证明AF=AG,再证明CE=2AG即可.
解答 (1)证明:∵∠BAD=∠CAE=90°,
∴∠BAD-∠CAD=∠CAE-∠CAD,
∴∠BAC=∠EAD,
在△ABC和△ADE中
$\left\{\begin{array}{l}{AB=AD}\\{∠BAC=∠DAE}\\{AC=AE}\end{array}\right.$,
∴△ABC≌△ADE(SAS).
(2)证明:∵∠CAE=90°,AC=AE
∴∠ACE=∠AEC=45°
∵△ABC≌△ADE
∴∠ACB=∠AEC=45°
∴∠ACB=∠ACE
∴AC平分∠ECF 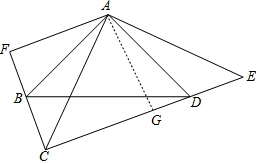
(3)解:结论:CE=2AF.
理由:过点A作AG⊥CG,垂足为点G
∵AC平分∠ECF,AF⊥CB,AG⊥CG,
∴AF=AG,
又∵AC=AE,AG⊥CG,
∴∠CAG=∠EAG=45°,
∴∠CAG=∠EAG=∠ACE=∠AEC=45°,
∴CG=AG=GE,
∴CE=2AG,
∴CE=2AF.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的性质、角平分线的性质定理等知识,解题的关键是熟练掌握全等三角形的判定和性质,学会添加常用辅助线,属于中考常考题型.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
4. 如图,射线AB∥射线CD,∠CAB与∠ACD的平分线交于点E,AC=4,点P是射线AB上的一动点,连结PE并延长交射线CD于点Q.给出下列结论:①△ACE是直角三角形;②S四边形APQC=2S△ACE;③设AP=x,CQ=y,则y关于x的函数表达式是y=-x+4(0≤x≤4),其中正确的是( )
如图,射线AB∥射线CD,∠CAB与∠ACD的平分线交于点E,AC=4,点P是射线AB上的一动点,连结PE并延长交射线CD于点Q.给出下列结论:①△ACE是直角三角形;②S四边形APQC=2S△ACE;③设AP=x,CQ=y,则y关于x的函数表达式是y=-x+4(0≤x≤4),其中正确的是( )
 如图,射线AB∥射线CD,∠CAB与∠ACD的平分线交于点E,AC=4,点P是射线AB上的一动点,连结PE并延长交射线CD于点Q.给出下列结论:①△ACE是直角三角形;②S四边形APQC=2S△ACE;③设AP=x,CQ=y,则y关于x的函数表达式是y=-x+4(0≤x≤4),其中正确的是( )
如图,射线AB∥射线CD,∠CAB与∠ACD的平分线交于点E,AC=4,点P是射线AB上的一动点,连结PE并延长交射线CD于点Q.给出下列结论:①△ACE是直角三角形;②S四边形APQC=2S△ACE;③设AP=x,CQ=y,则y关于x的函数表达式是y=-x+4(0≤x≤4),其中正确的是( )| A. | ①②③ | B. | ①② | C. | ①③ | D. | ②③ |


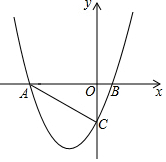 如图,抛物线y=ax2+bx+c交x轴于A(-4,0),B(1,0),交y轴于C点,且OC=2OB.
如图,抛物线y=ax2+bx+c交x轴于A(-4,0),B(1,0),交y轴于C点,且OC=2OB.