题目内容
【题目】已知函数
（
为常数且
）中，当
时，
；当
时，
．请对该函数及其图像进行如下探究：
（1）求该函数的解析式，并直接写出该函数自变量
的取值范围：
（2）请在下列直角坐标系中画出该函数的图像：
列表如下：
x | … | -4 | -3 | -2 | -1 | 0 |
|
| 1 | 2 | 3 | 4 | 5 | 6 | … |
y | … | … |
描点连线：
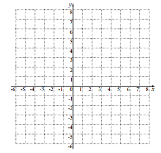
（3）请结合所画函数图象，写出函数图象的两条性质
（4）请你在上方直角坐标系中画出函数
的图像，结合上述函数的图像，写出不等式
的解集．
【答案】（1）
（2）见解析（3）见解析（答案不唯一，写出两条即可）（4）图象见解析；
或
【解析】
（1）根据题意解方程组即可得到结论；
（2）利用函数解析式分别求出对应的函数值即可，再利用描点法画出图象；
（3）通过观察图象，可以从曲线的增减性、所在象限、点的坐标等方面写一写图象性质；
（4）通过观察图象即可解决问题．
解：（1）已知函数
，当
时，
；当
时，
∴
∴
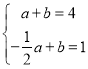
∴该函数解析式为；
（2）列表如下：
x | … | -4 | -3 | -2 | -1 | 0 |
|
| 1 | 2 | 3 | 4 | 5 | 6 | … |
y | … |
|
|
|
|
|
|
| \ |
|
|
|
|
| … |
描点连线：
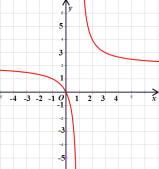
（3）①当
时，
随
的增大而减小；
②当
时，随的增大而减小；
③当
时，
；
④函数图象在第一、二、四象限；
（答案不唯一，写出两条即可）；
（4）如图：
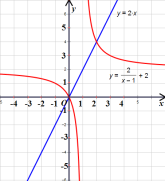
∵与
的交点为
、
∴结合函数图象可知，
的解集为或．
故答案是：（1）（2）见解析（3）见解析（答案不唯一，写出两条即可）（4）图象见解析；或
练习册系列答案
相关题目
