题目内容
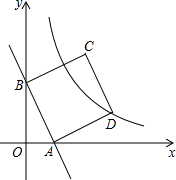 (2013•宛城区一模)如图,直线y=-2x+2与x轴y轴分别相交于点A、B,四边形ABCD是正方形,曲线y=
(2013•宛城区一模)如图,直线y=-2x+2与x轴y轴分别相交于点A、B,四边形ABCD是正方形,曲线y=| k | x |
3
3
.分析:作DE⊥x轴,垂足为E,连OD.证出△BOA≌△AED,得到AE=BO,AO=DE,从而求出S△DOE,根据反比例函数k的几何意义,求出k的值.
解答: 解:作DE⊥x轴,垂足为E,连OD.
解:作DE⊥x轴,垂足为E,连OD.
∵∠DAE+∠BAO=90°,∠OBA+∠BAO=90°,
∴∠DAE=∠OBA,
又∵∠BOA=∠AED,AB=DA,
∴△BOA≌△AED,
∴OA=DE.
∵y=-2x+2,可知B(0,2),A(1,0),
∴OA=DE=1,
∴OE=OA+AE=1+2=3,
∴S△DOE=
•OE•DE=
×3×1=
,
∴k=
×2=3.
故答案为3.
 解:作DE⊥x轴,垂足为E,连OD.
解:作DE⊥x轴,垂足为E,连OD.∵∠DAE+∠BAO=90°,∠OBA+∠BAO=90°,
∴∠DAE=∠OBA,
又∵∠BOA=∠AED,AB=DA,
∴△BOA≌△AED,
∴OA=DE.
∵y=-2x+2,可知B(0,2),A(1,0),
∴OA=DE=1,
∴OE=OA+AE=1+2=3,
∴S△DOE=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴k=
| 3 |
| 2 |
故答案为3.
点评:本题主要考查了反比例函数k的几何意义,构造△BOA≌△AED是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013•宛城区一模)某校九年级参加了“维护小区周边环境”、“维护繁华街道卫生”、“义务指路”等志愿者活动,如图是根据该校九年级六个班的同学某天“义务指路”总人次所绘制的折线统计图,则关于这六个数据中,下列说法正确的是( )
(2013•宛城区一模)某校九年级参加了“维护小区周边环境”、“维护繁华街道卫生”、“义务指路”等志愿者活动,如图是根据该校九年级六个班的同学某天“义务指路”总人次所绘制的折线统计图,则关于这六个数据中,下列说法正确的是( ) (2013•宛城区一模)某几何体的三视图如图所示,其中主视图和左视图均为边长为2的等边三角形,则该几何体的表面积为( )
(2013•宛城区一模)某几何体的三视图如图所示,其中主视图和左视图均为边长为2的等边三角形,则该几何体的表面积为( )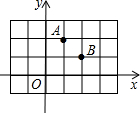 (2013•宛城区一模)点A,B均在由边长为1的相同小正方形组成的网格的格点上,建立平面直角坐标系如图所示,若P是x轴上使得|PA-PB|的值最大的点,Q是y轴上使得QA+QB的值最小的点,则OP+OQ=( )
(2013•宛城区一模)点A,B均在由边长为1的相同小正方形组成的网格的格点上,建立平面直角坐标系如图所示,若P是x轴上使得|PA-PB|的值最大的点,Q是y轴上使得QA+QB的值最小的点,则OP+OQ=( )