题目内容
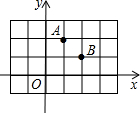（2013•宛城区一模）点A，B均在由边长为1的相同小正方形组成的网格的格点上，建立平面直角坐标系如图所示，若P是x轴上使得|PA-PB|的值最大的点，Q是y轴上使得QA+QB的值最小的点，则OP+OQ=（ ）分析：连接AB并延长交x轴于点P，作A点关于y轴的对称点A′连接A′B交y轴于点Q，求出点Q与y轴的交点坐标即可得出结论．
解答：
解：连接AB并延长交x轴于点P，由三角形的三边关系可知，点P即为x轴上使得|PA-PB|的值最大的点，
∵点B是正方形的中点，
∴点P即为AB延长线上的点，此时P（3，0）即OP=3；
作A点关于y轴的对称点A′连接A′B交y轴于点Q，则A′B即为QA+QB的最小值，
∵A′（-1，2），B（2，1），
设过A′B的直线为：y=kx+b，则
，
解得
，
∴Q（0，
），即OQ=
，
∴OP+OQ=3+
=
．
故选：C．
解：连接AB并延长交x轴于点P，由三角形的三边关系可知，点P即为x轴上使得|PA-PB|的值最大的点，∵点B是正方形的中点，
∴点P即为AB延长线上的点，此时P（3，0）即OP=3；
作A点关于y轴的对称点A′连接A′B交y轴于点Q，则A′B即为QA+QB的最小值，
∵A′（-1，2），B（2，1），
设过A′B的直线为：y=kx+b，则
|
解得
|
∴Q（0，
| 5 |
| 3 |
| 5 |
| 3 |
∴OP+OQ=3+
| 5 |
| 3 |
| 14 |
| 3 |
故选：C．
点评：本题考查的是轴对称-最短路线问题，根据题意得出P、Q两点的坐标是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
（2013•宛城区一模）某校九年级参加了“维护小区周边环境”、“维护繁华街道卫生”、“义务指路”等志愿者活动，如图是根据该校九年级六个班的同学某天“义务指路”总人次所绘制的折线统计图，则关于这六个数据中，下列说法正确的是（ ）
（2013•宛城区一模）某几何体的三视图如图所示，其中主视图和左视图均为边长为2的等边三角形，则该几何体的表面积为（ ）