题目内容
17．若S=（1-$\frac{1}{{2}^{2}}$）（1-$\frac{1}{{3}^{2}}$）（1-$\frac{1}{{4}^{2}}$）…（1-$\frac{1}{201{6}^{2}}$），则S的值为（ ）| A． | $\frac{2013}{2016}$ | B． | $\frac{2015}{2016}$ | C． | $\frac{2015}{4032}$ | D． | $\frac{2017}{4032}$ |
分析 原式各括号利用平方差公式分解后，约分即可得到结果．
解答 解：S=（1+$\frac{1}{2}$）（1-$\frac{1}{2}$）（1+$\frac{1}{3}$）（1-$\frac{1}{3}$）（1+$\frac{1}{4}$）（1-$\frac{1}{4}$）…（1+$\frac{1}{2016}$）（1-$\frac{1}{2016}$）
=$\frac{3}{2}$×$\frac{1}{2}$×$\frac{4}{3}$×$\frac{2}{3}$×$\frac{5}{4}$×$\frac{3}{4}$×…×$\frac{2017}{2016}$×$\frac{2015}{2016}$
=（$\frac{3}{2}$×$\frac{4}{3}$×$\frac{5}{4}$×…×$\frac{2017}{2016}$）×（$\frac{1}{2}$×$\frac{2}{3}$×$\frac{3}{4}$×…×$\frac{2015}{2016}$）
=$\frac{2017}{2}$×$\frac{1}{2016}$
=$\frac{2017}{4032}$，
故选D
点评 此题考查了平方差公式，熟练掌握平方差公式是解本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
12．在六张卡片上分别写有$\frac{1}{3}$，π，1.5，5，0，$\sqrt{2}$六个数，从中任意抽取一张，卡片上的数为无理数的概率是（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{5}{6}$ |
8．有40名大学毕业生在郊区承包了100亩土地，准备种植蔬菜、果树、药材，种植这几种作物每亩所需人数和预测利润见表：
请你设计一个种植方案，既要保证每亩地都种上作物，这40名大学毕业生都有工作，又要保证预测利润的总和最多．
| 作物名称 | 蔬菜 | 果树 | 药材 |
| 每亩地所需的人数（人） | $\frac{1}{2}$ | $\frac{1}{3}$ | $\frac{1}{4}$ |
| 每亩地的预测利润（元） | 11000 | 7500 | 6000 |
如图，已知AB∥CD，CA平分∠BCD，∠1=2∠2．求证：AD∥BC．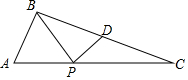
如图，△ABC中，AB=$\sqrt{5}$，AC=5，tanA=2，D是BC中点，点P是AC上一个动点，将△BPD沿PD折叠，折叠后的三角形与△PBC的重合部分面积恰好等于△BPD面积的一半，则AP的长为2或5-$\sqrt{5}$．
6．计算2-3的结果是（ ）
| A． | 1 | B． | 5 | C． | -5 | D． | -1 |
如图，已知直线l1：y=-2x+8与双曲线C：y=$\frac{6}{x}$（x＞0），相交于点A和B（点A在点B的左上方），直线l2：y=kx（k＞0）与直线l1相交于点C，于双曲线C相交于点D．（1）求点A、B的坐标；