题目内容
有理数a，b，c在数轴上的点如图所示，则
-
+
+
的值等于（ ）
| a-b |
| |a-b| |
| b-c |
| |b-c| |
| c-a |
| |c-a| |
| ab-ac |
| |ab-ac| |
| A、-1 | B、1 | C、2 | D、3 |
考点：绝对值,数轴
专题：
分析：先根据数轴，求出a、b、c的取值范围，依此确定a-b，b-c，c-a，ab-ac取值范围，再去绝对值符号计算即可．
解答：解：根据数轴得
a＜b＜0＜c，
则a-b＜0，b-c＜0，c-a＞0，ab-ac＞0，
则
-
+
+
=-1+1+1+1=2．
故选：C．
a＜b＜0＜c，
则a-b＜0，b-c＜0，c-a＞0，ab-ac＞0，
则
| a-b |
| |a-b| |
| b-c |
| |b-c| |
| c-a |
| |c-a| |
| ab-ac |
| |ab-ac| |
故选：C．
点评：此题考查了数轴的内容、有理数的混合运算，绝对值的性质，体现了数形结合的优点．
练习册系列答案
阅读快车系列答案
相关题目
下列代数式中能用平方差公式分解因式的是（ ）
| A、a2+b2 |
| B、-a2-b2 |
| C、a2-c2-2ac |
| D、-4a2+b2 |
函数y=ax-3的图象与y=bx+4的图象交于x轴上一点，那么a：b等于（ ）
| A、-4：3 |
| B、4：3 |
| C、（-3）：（-4） |
| D、3：（-4） |
计算：（x+1）（2x-1）的结果是（ ）
| A、2x2+2x-1 |
| B、2x2-2x-1 |
| C、2x2+x |
| D、2x2+x-1 |
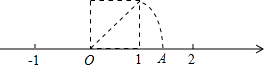如图，以数轴的单位长线段为边作一个正方形，以数轴的原点为圆心，正方形的对角线长为半径画弧，交数轴于点A，点A表示数x，则x2的平方根是（ ）
如图，AB是⊙O的直径，C是⊙O上一点，AD⊥CD于D，BE⊥CD于E，BC平分∠ABE，连接AC、BC．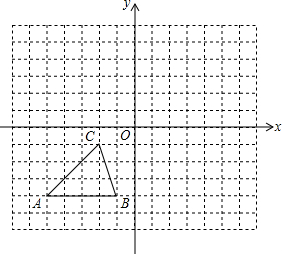
如图，方格纸中的每个小方格都是边长为1个单位的正方形，每个小正方形的顶点叫格点．已知△ABC的顶点均在格点上，在建立平面直角坐标系后，点B的坐标为l2．