题目内容
 矩形ABCD沿AE折叠,使点D落在BC边上的F点处,如果∠BAF=60°,则∠DAE等于( )
矩形ABCD沿AE折叠,使点D落在BC边上的F点处,如果∠BAF=60°,则∠DAE等于( )| A、15° | B、30° |
| C、45° | D、60 |
考点:翻折变换(折叠问题)
专题:
分析:根据矩形的每一个角都是直角求出∠DAF,再根据翻折变化的性质可得∠DAE=∠EAF,然后求解即可.
解答:解:∵四边形ABCD是矩形,
∴∠BAD=90°,
∵∠BAF=60°,
∴∠DAF=∠BAD-∠BAF=90°-60°=30°,
由翻折的性质得,∠DAE=∠EAF,
∴∠DAE=
×30°=15°.
故选A.
∴∠BAD=90°,
∵∠BAF=60°,
∴∠DAF=∠BAD-∠BAF=90°-60°=30°,
由翻折的性质得,∠DAE=∠EAF,
∴∠DAE=
| 1 |
| 2 |
故选A.
点评:本题考查了翻折变换的性质,矩形的性质,是基础题,熟记性质各是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
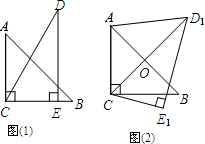 把一副三角板如图(1)放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=4,CD=5.把三角板DCE绕着点C顺时针旋转15°得到△D1CE1(如图2),此时AB与CD1交于点O,则线段AD1的长度为( )
把一副三角板如图(1)放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=4,CD=5.把三角板DCE绕着点C顺时针旋转15°得到△D1CE1(如图2),此时AB与CD1交于点O,则线段AD1的长度为( )A、
| ||
B、
| ||
C、2
| ||
| D、4 |
下列四个算式中,正确的个数有( )
①a4•a3=a12 ②a5+a5=a10 ③a5•a5=a10 ④(a3)3=a6.
①a4•a3=a12 ②a5+a5=a10 ③a5•a5=a10 ④(a3)3=a6.
| A、0个 | B、1个 | C、2个 | D、3个 |
计算(-4)2的值是( )
| A、16 | B、-16 | C、8 | D、-8 |
 如图,⊙O是△ABC的外接圆,且∠BAO=25°,则∠C的度数为
如图,⊙O是△ABC的外接圆,且∠BAO=25°,则∠C的度数为