题目内容
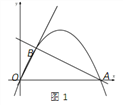
【题目】如图,在平面直角坐标系xOy中,拋物线![]() 与x轴交于O,A,点B在抛物线上且横坐标为2.
与x轴交于O,A,点B在抛物线上且横坐标为2.
(1)如图1,△AOB的面积是多少?
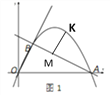
(2)如图1,在线段AB上方的抛物线上有一点K,当△ABK的面积最大时,求点K的坐标及△ABK的面积;
(3)在(2)的条件下,点H 在y轴上运动,点I在x轴上运动. 则当四边形BHIK周长最小时,求出H、I的坐标以及四边形BHIK周长的最小值.
【答案】(1)![]() ;(2)当
;(2)当![]() 有最大值16.
有最大值16.
【解析】分析:(1)把点B的横坐标2![]() 求出纵坐标4,然后利用三角形面积公式计算即可;(2)设点K(
求出纵坐标4,然后利用三角形面积公式计算即可;(2)设点K(![]() ),求出直线AB的解析式为:
),求出直线AB的解析式为: ![]() ,进而求出点M(m,
,进而求出点M(m, ![]() ),表示出
),表示出![]() 的面积化为顶点式即可求解;(3)作B点关于y轴对称点
的面积化为顶点式即可求解;(3)作B点关于y轴对称点![]() ,作K点关于x轴的对称点
,作K点关于x轴的对称点![]() ,连接
,连接![]() ,求出
,求出![]() ,
, ![]() 的解析式,利用最短路径求解.
的解析式,利用最短路径求解.
本题解析:
(1)当![]() 时,得
时,得![]() ; 当
; 当![]() 时,
时, ![]() ,所以
,所以![]()
(2)过K作![]()
![]() ,
, ![]()
![]() , ∴直线AB的解析式为:
, ∴直线AB的解析式为: ![]()
![]() ,
, ![]()
![]() ,
, ![]() =16.
=16.
(3)作B点关于y轴对称点![]() (-2,4),作K点关于x轴的对称点
(-2,4),作K点关于x轴的对称点![]() (6,-6),连接
(6,-6),连接![]() ,分别交y轴x轴于H,I两点,此时四边形BHIK的周长最小.
,分别交y轴x轴于H,I两点,此时四边形BHIK的周长最小.
![]()
![]()
∴四边形BHIK周长的最小值为![]() .
.

 阅读快车系列答案
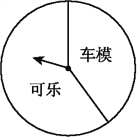
阅读快车系列答案【题目】某商场“六一”期间进行一个有奖销售的活动,设立了一个可以自由转动的转盘(如图),并规定:顾客购物100元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品(若指针落在两个区域的交界处,则重新转动转盘).下表是此次促销活动中的一组统计数据:
转动转盘的次数n | 100 | 200 | 400 | 500 | 800 | 1 000 |
落在“可乐”区域 的次数m | 60 | 122 | 240 | 298 | 604 | |
落在“可乐” 区域的频率 | 0.6 | 0.61 | 0.6 | 0.59 | 0.604 |
(1)计算并完成上述表格;
(2)请估计当n很大时,频率将会接近__________;假如你去转动该转盘一次,你获得“可乐”的概率约是__________;(结果精确到0.1)
(3)在该转盘中,表示“车模”区域的扇形的圆心角约是多少度?