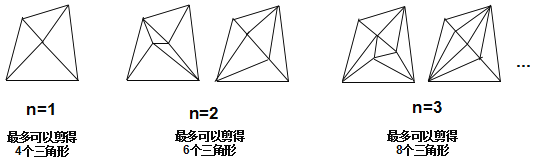
ЬтФПФкШн
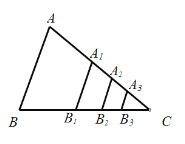
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯBЃН90ЁуЃЌACЃН60 cmЃЌЁЯAЃН60ЁуЃЌЕуDДгЕуCГіЗЂбиCAЗНЯђвд4 cm/УыЕФЫйЖШЯђЕуAдШЫйдЫЖЏЃЌЭЌЪБЕуEДгЕуAГіЗЂбиABЗНЯђвд2 cm/УыЕФЫйЖШЯђЕуBдШЫйдЫЖЏЃЌЕБЦфжавЛИіЕуЕНДяжеЕуЪБЃЌСэвЛИіЕувВЫцжЎЭЃжЙдЫЖЏЃЎЩшЕуDЃЌEдЫЖЏЕФЪБМфЪЧtУы(0<tЁм15)ЃЎЙ§ЕуDзїDFЁЭBCгкЕуFЃЌСЌНгDEЃЌEF.
(1)ЧѓжЄЃКAEЃНDFЃЛ
(2)ЫФБпаЮAEFDФмЙЛГЩЮЊСтаЮТ№ЃПШчЙћФмЃЌЧѓГіЯргІЕФtжЕЃЛШчЙћВЛФмЃЌЧыЫЕУїРэгЩЃЛ
(3)ЕБtЮЊКЮжЕЪБЃЌЁїDEFЮЊжБНЧШ§НЧаЮЃПЧыжБНгаДГіНсЙћЃЛ

ЁОД№АИЁПЃЈ1ЃЉЯъМћНтЮіЃЛЃЈ2ЃЉФмЃЌЕБtЃН10УыЪБЃЌЫФБпаЮAEFDЮЊСтаЮЃЛЃЈ3ЃЉЕБtЃН![]() Лђ12УыЪБЃЌЁїDEFЮЊжБНЧШ§НЧаЮЃЎ
Лђ12УыЪБЃЌЁїDEFЮЊжБНЧШ§НЧаЮЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУtБэЪОГіCDвдМАAEЕФГЄЃЌШЛКѓдкжБНЧЁїCDFжаЃЌРћгУжБНЧШ§НЧаЮЕФаджЪЧѓЕУDFЕФГЄЃЌМДПЩжЄУї.
ЃЈ2ЃЉвзжЄЫФБпаЮAEFDЪЧЦНааЫФБпаЮЃЌЕБAD=AEЪБЃЌЫФБпаЮAEFDЪЧСтаЮЃЌОнДЫМДПЩСаЗНГЬЧѓЕУtЕФжЕ.
ЃЈ3ЃЉЁїDEFЮЊжБНЧШ§НЧаЮЂйЕБЁЯDEFЃН90ЁуЪБЃЌгЩ(2)жЊЫФБпаЮAEFDЮЊЦНааЫФБпаЮЃЌвзЧѓADЃН![]() AEЃНtЃЌгжADЃН60Ѓ4tЃЌМД60Ѓ4tЃНtЃЌМДПЩНтЕУДЫЪБtЃН12ЃЛЂкЕБЁЯEDFЃН90ЁуЪБЃЌЫФБпаЮEBFDЮЊОиаЮЃЌвзЧѓADЃН2AEЃЌМД60Ѓ4tЃН4tЃЌНтЕУДЫЪБtЃН
AEЃНtЃЌгжADЃН60Ѓ4tЃЌМД60Ѓ4tЃНtЃЌМДПЩНтЕУДЫЪБtЃН12ЃЛЂкЕБЁЯEDFЃН90ЁуЪБЃЌЫФБпаЮEBFDЮЊОиаЮЃЌвзЧѓADЃН2AEЃЌМД60Ѓ4tЃН4tЃЌНтЕУДЫЪБtЃН![]() ЃЛЂлШєЁЯEFDЃН90ЁуЃЌдђEгыBжиКЯЃЌDгыAжиКЯЃЌДЫжжЧщПіВЛДцдкЃЎ
ЃЛЂлШєЁЯEFDЃН90ЁуЃЌдђEгыBжиКЯЃЌDгыAжиКЯЃЌДЫжжЧщПіВЛДцдкЃЎ
(1)жЄУїЃКдкЁїDFCжаЃЌЁЯDFCЃН90ЁуЃЌЁЯCЃН30ЁуЃЌDCЃН4t
ЁрDFЃН2t
гжЁпAEЃН2t
ЁрAEЃНDF.
(2)ФмЃЎРэгЩШчЯТЃК
ЁпABЁЭBCЃЌDFЁЭBC
ЁрAEЁЮDF
гжЁпAEЃНDF
ЁрЫФБпаЮAEFDЮЊЦНааЫФБпаЮЃЎ
ЕБЫФБпаЮAEFDЮЊСтаЮЪБЃЌAEЃНADЃНACЃDC
МД60Ѓ4tЃН2tЃЌ
НтЕУtЃН10.
ЁрЕБtЃН10УыЪБЃЌЫФБпаЮAEFDЮЊСтаЮЃЎ
(3)ЂйЕБЁЯDEFЃН90ЁуЪБЃЌгЩ(2)жЊЫФБпаЮAEFDЮЊЦНааЫФБпаЮЃЌ
ЁрEFЁЮAD
ЁрЁЯADEЃНЁЯDEFЃН90Ёу
ЁпЁЯAЃН60Ёу
ЁрЁЯAEDЃН30Ёу
ЁрADЃН![]() AEЃНt.
AEЃНt.
гжADЃН60Ѓ4tЃЌМД60Ѓ4tЃНtЃЌНтЕУtЃН12ЃЛ
ЂкЕБЁЯEDFЃН90ЁуЪБЃЌЫФБпаЮEBFDЮЊОиаЮЃЌдкRtЁїAEDжаЃЌЁЯAЃН60Ёу
дђЁЯADEЃН30Ёу
ЁрADЃН2AEЃЌМД60Ѓ4tЃН4tЃЌНтЕУtЃН![]() ЃЛ
ЃЛ
ЂлШєЁЯEFDЃН90ЁуЃЌдђEгыBжиКЯЃЌDгыAжиКЯЃЌДЫжжЧщПіВЛДцдкЃЎ
ЙЪЕБtЃН![]() Лђ12УыЪБЃЌЁїDEFЮЊжБНЧШ§НЧаЮЃЎ
Лђ12УыЪБЃЌЁїDEFЮЊжБНЧШ§НЧаЮЃЎ

ЁОЬтФПЁПНќМИФъЃЌЫцзХЕчзгЩЬЮёЕФПьЫйЗЂеЙЃЌЁАЕчЩЬАќЙќМўЁБеМЁАПьЕнМўЁБзмСПЕФБШР§ж№ФъдіГЄЃЌИљОнЦѓвЕВЦБЈЃЌФГЭјеОЕУЕНШчЯТЭГМЦБэЃК
ФъЗн | 2014 | 2015 | 2016 | 2017ЃЈдЄМЦЃЉ |
ПьЕнМўзмСПЃЈвкМўЃЉ | 140 | 207 | 310 | 450 |
ЕчЩЬАќЙќМўЃЈвкМўЃЉ | 98 | 153 | 235 | 351 |
ЃЈ1ЃЉЧыбЁдёЪЪЕБЕФЭГМЦЭМЃЌУшЪі2014Љ2017ФъЁАЕчЩЬАќЙќМўЁБеМЕБФъЁАПьЕнМўЁБзмСПЕФАйЗжБШЃЈОЋШЗЕН1%ЃЉЃЛ
ЃЈ2ЃЉШє2018ФъЁАПьЕнМўЁБзмСПНЋДяЕН675вкМўЃЌЧыЙРМЦЦфжаЁАЕчЩЬАќЙќМўЁБдМЮЊЖрЩйвкМўЃП