题目内容
【题目】(教材回顾)
七上教材有这样一段文字:人们通过长期观察发现如果早晨天空中棉絮的高积云,那么午后常有雷雨降临,于是有了“朝有破絮云,午后雷雨临”的谚语.在数学的学习过程中,我们经常用这样的方法探究规律.
(数学问题)
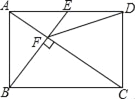
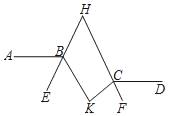
四边形有4个顶点,如果在它的内部再画n个点,并以这(n+4)个点为顶点画三角形,那么最多可以剪得多少个这样的三角形?
(问题探究)
为了解决这个问题,我们可以从n=1,n=2,n=3等具体的、简单的情形入手,探索最多可以剪得的三角形个数的变化规律.
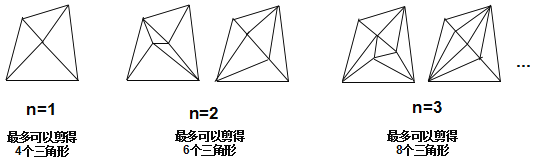
(问题解决)
(1)当四边形内有4个点时,最多剪得的三角形个数为______________;
(2)你发现的变化规律是:四边形内的点每增加1个,最多剪得的三角形增加______个;
(3)猜想:当四边形内点的个数为n时,最多可以剪得_______________个三角形;像这样通过对简单情形的观察、分析,从特殊到一般地探索这类现象的规律、提出猜想的思想方法称为归纳.
(问题拓展)
请你尝试用归纳的方法探索4+6+8+10+…+2n+(2n+2)的和是多少?
【答案】(1)10;(2)2;(3)2n+2;问题拓展:n2+3n.
【解析】
(1)根据【问题探究】提供的数据,进而得出答案;
(2)利用探究数据得出三角形个数的变化规律即可;
(3)因为6-4=8-6=2,所以四边形内的点每增加1个,最多可以剪得的三角形增加2个;∵四边形内点的个数为1时,最多剪出的小三角形个数4=2×1+2,因为四边形内点的个数为2时,最多剪出的小三角形个数6=2×2+2,四边形内点的个数为3时,最多剪出的小三角形个数8=2×3+2,所以四形内点的个数为n时,最多剪出的小三角形个数2n+2;
[问题拓展]列表归纳即可得到结论.
(1)∵当四边形内点的个数为1时,最多可以剪得4个三角形;
当四形内点的个数为2时,最多可以剪得6个三角形;
当四边形内点的个数为3时,最多可以剪得8个三角形;
当四边形内点的个数为4时,最多可以剪得10个三角形;
(2)利用(1)中变化规律得出:因为6-4=8-6=2,所以四边形内的点每增加1个,最多可以剪得的三角形增加2个;
(3)∵四边形内点的个数为1时,最多剪出的小三角形个数4=2×1+2,因为四边形内点的个数为2时,最多剪出的小三角形个数6=2×2+2,四边形内点的个数为3时,最多剪出的小三角形个数8=2×3+2,所以四形内点的个数为n时,最多剪出的小三角形个数2n+2;
[问题拓展]
列表归纳
加数的个数 | 和 |
4+6 | 22+2×3 |
4+6+8 | 32+3×3 |
4+6+8+10 | 42+4×3 |
… | … |
4+6+8+10+…+(2n+2) | n2+3n |
∴4+6+8+10+…+2n+(2n+2)= n2+3n

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】王华、张伟两位同学分别将自己10次数学自我检测的成绩绘制成如下统计图:
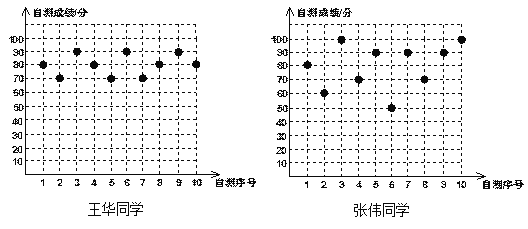
(1)根据上图中提供的数据列出如下统计表:
平均成绩(分) | 中位数(分) | 众数(分) | 方差(S2) | |
王华 | 80 | b | 80 | d |
张伟 | a | 85 | c | 260 |
则a= ,b= ,c= ,d= ,
(2)将90分以上(含90分)的成绩视为优秀,则优秀率高的是 .
(3)现在要从这两个同学选一位去参加数学竞赛,你可以根据以上的数据给老师哪些建议?