题目内容
 如图,AD=AE,BD=CE,∠ADB=∠AEC=100°,∠BAE=70°,下列结论:
如图,AD=AE,BD=CE,∠ADB=∠AEC=100°,∠BAE=70°,下列结论:
①△ABE≌△ACD;②△ABD≌△ACE;③∠DAE=40°;④∠C=30°.
其中正确的结论是________(填序号)
①②④
分析:根据SAS即可推出△ABD≌△ACE,推出AB=AC,∠B=∠C,求出BE=DC,根据SSS推出△ABE≌△ACD,推出∠BAE=∠CAD=70°,根据三角形外角性质即可求出C,求出∠EAC,即可求出∠DAE.
解答:∵在△ABD和△ACE中

∴△ABD≌△ACE,∴②正确;
∴AB=AC,∠B=∠C,
∵BD=CE,
∴BD+DE=EC+DE,
∴BE=DC,
在△ABE和△ACD中

∴△ABE≌△ACD,∴①正确;
∴∠BAE=∠CAD=70°,
∵∠ADB=100°,
∴∠C=∠ADB-∠CAD=100°-70°=30°,∴④正确;
∴∠EAC=180°-∠C-∠AEC=180°-30°-100°=50°,
∴∠DAE=∠CAD-∠EAC=70°-50°=20°,∴③错误;
故答案为:①②④.
点评:本题考查了全等三角形的性质和判定,三角形外角性质,三角形内角和定理的应用,主要考查学生的推理能力.
分析:根据SAS即可推出△ABD≌△ACE,推出AB=AC,∠B=∠C,求出BE=DC,根据SSS推出△ABE≌△ACD,推出∠BAE=∠CAD=70°,根据三角形外角性质即可求出C,求出∠EAC,即可求出∠DAE.
解答:∵在△ABD和△ACE中

∴△ABD≌△ACE,∴②正确;
∴AB=AC,∠B=∠C,
∵BD=CE,
∴BD+DE=EC+DE,
∴BE=DC,
在△ABE和△ACD中

∴△ABE≌△ACD,∴①正确;
∴∠BAE=∠CAD=70°,
∵∠ADB=100°,
∴∠C=∠ADB-∠CAD=100°-70°=30°,∴④正确;
∴∠EAC=180°-∠C-∠AEC=180°-30°-100°=50°,
∴∠DAE=∠CAD-∠EAC=70°-50°=20°,∴③错误;
故答案为:①②④.
点评:本题考查了全等三角形的性质和判定,三角形外角性质,三角形内角和定理的应用,主要考查学生的推理能力.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目
 2、如图,AD=AE,∠1=∠2,BD=CE,则有△ABD≌△
2、如图,AD=AE,∠1=∠2,BD=CE,则有△ABD≌△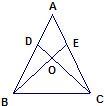 21、已知:如图,AD=AE,∠ADC=∠AEB,BE与CD相交于O点.
21、已知:如图,AD=AE,∠ADC=∠AEB,BE与CD相交于O点. 39、已知:如图,AD=AE,AB=AC,BD、CE相交于O.
39、已知:如图,AD=AE,AB=AC,BD、CE相交于O. 23、已知:如图,AD=AE,AB=AC,DC与BE交于O点.
23、已知:如图,AD=AE,AB=AC,DC与BE交于O点. 如图,AD=AE,AB=AC,∠A=60°,∠C=25°,则∠DOB=
如图,AD=AE,AB=AC,∠A=60°,∠C=25°,则∠DOB=