题目内容
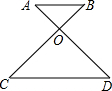 已知AB∥CD,AD、BC交于点O,已知AO=2,DO=4,CD=5,求AB的长.
已知AB∥CD,AD、BC交于点O,已知AO=2,DO=4,CD=5,求AB的长.
解:∵AB∥CD,
∴∠A=∠D,∠B=∠C,
∴△AOB∽△DOC,
∴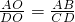 ,即
,即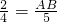 ,
,
∴AB=2.5.
分析:根据已知条件证明△AOB∽△DOC,再根据相似三角形的对应边成比例的性质列出等式,从而求得AB的长.
点评:本题主要考查了相似三角形的判定及性质:有两角对应相等的两个三角形相似;相似三角形的三边对应成比例.
∴∠A=∠D,∠B=∠C,
∴△AOB∽△DOC,
∴
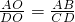 ,即
,即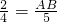 ,
,∴AB=2.5.
分析:根据已知条件证明△AOB∽△DOC,再根据相似三角形的对应边成比例的性质列出等式,从而求得AB的长.
点评:本题主要考查了相似三角形的判定及性质:有两角对应相等的两个三角形相似;相似三角形的三边对应成比例.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
 2、如图,已知AB∥CD,AD与BC相交于点O,AO:DO=1:2,那么下列式子错误的是( )
2、如图,已知AB∥CD,AD与BC相交于点O,AO:DO=1:2,那么下列式子错误的是( )
 47、如图,已知AB∥CD,AD∥BC,回答下来问题.
47、如图,已知AB∥CD,AD∥BC,回答下来问题. (2013•东营)如图,已知AB∥CD,AD和BC相交于点O,∠A=50°,∠AOB=105°,则∠C等于( )
(2013•东营)如图,已知AB∥CD,AD和BC相交于点O,∠A=50°,∠AOB=105°,则∠C等于( ) 如图,已知AB=CD,AD=CB,你能得到AD∥BC,AB∥CD的结论?为什么?
如图,已知AB=CD,AD=CB,你能得到AD∥BC,AB∥CD的结论?为什么?