题目内容
【题目】如图,抛物线y=﹣ ![]() x2+bx+e与x轴交于点A(﹣3,0)、点B(9,0),与y轴交于点C,顶点为D,连接AD、DB,点P为线段AD上一动点.
x2+bx+e与x轴交于点A(﹣3,0)、点B(9,0),与y轴交于点C,顶点为D,连接AD、DB,点P为线段AD上一动点.
(1)求抛物线的解析式;
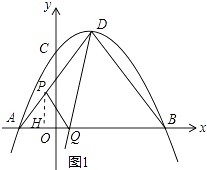
(2)如图1,过点P作BD的平行线,交AB于点Q,连接DQ,设AQ=m,△PDQ的面积为S,求S关于m的函数解析式,以及S的最大值;
(3)如图2,抛物线对称轴与x轴交与点G,E为OG的中点,F为点C关于DG对称的对称点,过点P分别作直线EF、DG的垂线,垂足为M、N,连接MN,直接写出△PMN为等腰三角形时点P的坐标.
【答案】
(1)
解:∵a=﹣ ![]() ,抛物线与x轴交与点A(﹣3,0),点B(9,0),
,抛物线与x轴交与点A(﹣3,0),点B(9,0),
∴可以假设抛物线解析式为y=﹣ ![]() (x+3)(x﹣9)=﹣
(x+3)(x﹣9)=﹣ ![]() x2+
x2+ ![]() x+6,
x+6,
∴抛物线解析式为y=﹣ ![]() x2+
x2+ ![]() x+6,
x+6,
(2)
解:∵y=﹣ ![]() x2+
x2+ ![]() x+6=﹣
x+6=﹣ ![]() (x﹣3)2+8,
(x﹣3)2+8,
∴顶点D坐标(3,8),
∵AD=DB=10,
∴∠DAB=∠DBA,
∵PQ∥BD,
∴∠PQA=∠DBA,
∴∠PAQ=∠PQA,
∴PA=PQ,
∴△PAQ为等腰三角形,
作PH⊥AQ于H,则AH=HQ= ![]() (如图1中),
(如图1中),
∴tan∠DAB= ![]() =
= ![]() ,
,
∴PH= ![]() m,
m,
∴S=S△ADQ﹣S△APQ= ![]() m8﹣
m8﹣ ![]() m
m ![]() m=﹣
m=﹣ ![]() m2+4m=﹣
m2+4m=﹣ ![]() (m﹣6)2+12,
(m﹣6)2+12,
∴当m=6时,S最大值=12.
(3)
解:∵E( ![]() ,0),F(6,6),
,0),F(6,6),
∴直线EF解析式为y= ![]() x﹣2,直线AD解析式为y=
x﹣2,直线AD解析式为y= ![]() x+4,
x+4,
∴EF∥AD,作EL⊥AD于L,(如图2中)
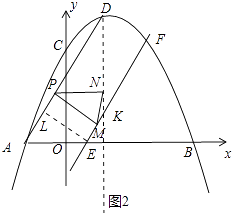
∵AE= ![]() ,sin∠DAB=
,sin∠DAB= ![]() ,
,
∴LE= ![]() ×
× ![]() =
= ![]() =PM,
=PM,
①PM=PN= ![]() 时,
时,
∴xP=3﹣ ![]() =﹣
=﹣ ![]() ,yP=﹣
,yP=﹣ ![]() ×
× ![]() +4=
+4= ![]() ,
,
∴P(﹣ ![]() ,
, ![]() ),
),
∴直线PM解析式为y=﹣ ![]() x+
x+ ![]() ,
,
由 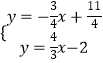 ,解得
,解得 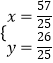 ,
,
∴点M( ![]() ,
, ![]() )
)
∴EM= ![]() =
= ![]() .
.
②NP=NM时,设直线EF与对称轴交于点K,K(3,2),
此时点N在PM的垂直平分线上,DN=NK,
∴N(3,5),P( ![]() ,5),
,5),
∴直线PM的解析式为y=﹣ ![]() x+
x+ ![]() ,
,
由 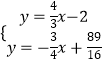 ,解得
,解得 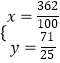 ,
,
∴M( ![]() ,
, ![]() ),
),
∴EM= ![]() =
= ![]() ,
,
③PM=MN时,cos∠MPN= ![]() =
= ![]() ,
,
∴PN= ![]() ,由此可得P(﹣
,由此可得P(﹣ ![]() ,
, ![]() ),
),
∴直线PM解析式为y=﹣ ![]() x﹣
x﹣ ![]() ,
,
由 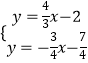 解得
解得 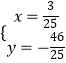 ,
,
∴M( ![]() ,﹣
,﹣ ![]() ),
),
∴EM= ![]() =
= ![]() .
.
综上所述,EM= ![]() 或
或 ![]() 或
或 ![]() .
.
【解析】(1)可以假设抛物线解析式为y=﹣ ![]() (x+3)(x﹣9),展开化简即可.(2)作PH⊥AQ于H,则AH=HQ=
(x+3)(x﹣9),展开化简即可.(2)作PH⊥AQ于H,则AH=HQ= ![]() (如图1中),根据S=S△ADQ﹣S△APQ构建二次函数,利用二次函数的性质即可解决问题.(3)分三种情形讨论①PM=PN,②NP=NM,③MN=MP,分别求出直线PM的解析式,利用方程组求出点M坐标即可解决问题.
(如图1中),根据S=S△ADQ﹣S△APQ构建二次函数,利用二次函数的性质即可解决问题.(3)分三种情形讨论①PM=PN,②NP=NM,③MN=MP,分别求出直线PM的解析式,利用方程组求出点M坐标即可解决问题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】绿色无公害蔬菜基地有甲、乙两种植户,他们种植了A,B两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如下表:
种植户 | 种植A类蔬菜面积 | 种植B类蔬菜面积 | 总收入 |
甲 | 3 | 1 | 12500 |
乙 | 2 | 3 | 16500 |
说明:不同种植户种植的同类蔬菜每亩的平均收入相等;亩为土地面积单位.
(1)求A、B两类蔬菜每亩的平均收入各是多少元;
(2)某种植户准备租20亩地用来种植A、B两类蔬菜,为了使总收入不低于63000元,且种植A类蔬菜的面积多于种植B类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户所有租地方案.
【题目】现要把192吨物资从我市运往甲、乙两地,用大、小两种货车共18辆恰好能一次性运完这批物资.已知这两种货车的载重量分别为14吨/辆和8吨/辆,运往甲、乙两地的运费如表:
运往地 | 甲地(元/辆) | 乙地(元/辆) |
大货车 | 720 | 800 |
小货车 | 500 | 650 |
(1)求这两种货车各用多少辆?
(2)如果安排10辆货车前往甲地,其余货车前往乙地,其中前往甲地的大货车为a辆,前往甲、乙两地的总运费为w元,求出w与a的函数关系式;
(3)在(2)的条件下,若运往甲地的物资部少于96吨,请你设计出使总运费最低的货车调配方案,并求出最少总运费.