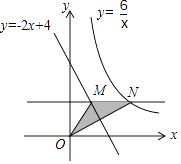��Ŀ����
����Ŀ����ͼ����ԭ���ֱ��y=k1x��y=k2x�뷴��������y= ![]() ��ͼ��ֱ�������A��C��B��D������AB��BC��CD��DA��
��ͼ��ֱ�������A��C��B��D������AB��BC��CD��DA��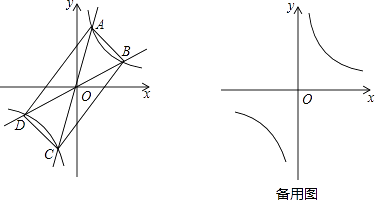
��1���ı���ABCDһ�����ı��Σ���ֱ����д�����
��2���ı���ABCD�����Ǿ����������ܣ������ʱk1 �� k2֮��Ĺ�ϵʽ�������ܣ�˵�����ɣ�
��3����P��x1 �� y1����Q��x2 �� y2����x2��x1��0���Ǻ���y= ![]() ͼ���ϵ��������㣬a=
ͼ���ϵ��������㣬a= ![]() ��b=
��b= ![]() �����ж�a��b�Ĵ�С��ϵ����˵�����ɣ�
�����ж�a��b�Ĵ�С��ϵ����˵�����ɣ�
���𰸡�
��1��ƽ��
��2��
�⣺������������y=k1x��k1��0���뷴��������y= ![]() ��ͼ���ڵ�һ�����ཻ��A��
��ͼ���ڵ�һ�����ཻ��A��
��k1x= ![]() �����x=
�����x= ![]() ����Ϊ���ڵ�һ���ޣ����Ը�����ȥ��ֻ����������
����Ϊ���ڵ�һ���ޣ����Ը�����ȥ��ֻ����������
��x= ![]() ����y=k1x��y=
����y=k1x��y= ![]() ��
��
��A��������� ![]() ��
�� ![]() ��ͬ����B������Ϊ��
��ͬ����B������Ϊ�� ![]() ��
�� ![]() ����
����
�֡�OA=OB��
�� ![]() =
= ![]() ������ƽ���ã�
������ƽ���ã� ![]() +k1=
+k1= ![]() +k2��
+k2��
������ã�k1��k2����k1k2��1��=0��
��k1��k2��
����k1k2��1=0����k1k2=1��
��3��
�⣺��P��x1��y1����Q��x2��y2����x2��x1��0���Ǻ���y= ![]() ͼ���ϵ��������㣬
ͼ���ϵ��������㣬
��y1= ![]() ��y2=
��y2= ![]() ��
��
��a= ![]() =
= ![]() =
= ![]() ��
��
��a��b= ![]() ��
�� ![]() =
= ![]() =
= ![]() ��
��
��x2��x1��0��
�� ![]() ��0��x1x2��0����x1+x2����0��
��0��x1x2��0����x1+x2����0��
�� ![]() ��0��
��0��
��a��b��0��
��a��b��
���������⣺��1����ֱ��y=k1x��y=k2x�뷴��������y= ![]() ��ͼ�����ԭ��Գƣ�
��ͼ�����ԭ��Գƣ�
��OA=OC��OB=OD��
���ı���ABCD ��ƽ���ı��Σ�
���Դ��ǣ�ƽ�У�