题目内容
【题目】如图,已知抛物线y=x2+bx+c与x轴交于A、B两点(A点在B点左侧),与y轴交于点C(0,﹣3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.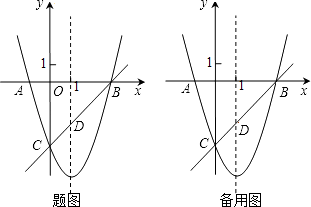
(1)求抛物线的函数表达式;
(2)求直线BC的函数表达式;
(3)点E为y轴上一动点,CE的垂直平分线交CE于点F,交抛物线于P、Q两点,且点P在第三象限.
①当线段PQ= ![]() AB时,求tan∠CED的值;
AB时,求tan∠CED的值;
②当以点C、D、E为顶点的三角形是直角三角形时,请直接写出点P的坐标.
温馨提示:考生可以根据第(3)问的题意,在图中补出图形,以便作答.
【答案】
(1)
解:∵抛物线的对称轴为直线x=1,
∴ ![]()
∴b=﹣2
∵抛物线与y轴交于点C(0,﹣3),
∴c=﹣3,
∴抛物线的函数表达式为y=x2﹣2x﹣3;
(2)
解:∵抛物线与x轴交于A、B两点,
当y=0时,x2﹣2x﹣3=0.
∴x1=﹣1,x2=3.
∵A点在B点左侧,
∴A(﹣1,0),B(3,0)
设过点B(3,0)、C(0,﹣3)的直线的函数表达式为y=kx+m,
则 ![]() ,∴
,∴ ![]()
∴直线BC的函数表达式为y=x﹣3;
(3)
解:
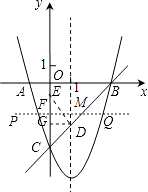
①∵AB=4,PQ= ![]() AB,
AB,
∴PQ=3
∵PQ⊥y轴
∴PQ∥x轴,
则由抛物线的对称性可得PM= ![]() ,
,
∵对称轴是直线x=1,
∴P到y轴的距离是 ![]() ,
,
∴点P的横坐标为 ![]() ,
,
∴P( ![]() ,
, ![]() )
)
∴F(0, ![]() ),
),
∴FC=3﹣OF=3﹣ ![]() =
= ![]()
∵PQ垂直平分CE于点F,
∴CE=2FC= ![]()
∵点D在直线BC上,
∴当x=1时,y=﹣2,则D(1,﹣2),
过点D作DG⊥CE于点G,
∴DG=1,CG=1,
∴GE=CE﹣CG= ![]() ﹣1=
﹣1= ![]() .
.
在Rt△EGD中,tan∠CED= ![]() .
.
②P1(1﹣ ![]() ,﹣2),P2(1﹣
,﹣2),P2(1﹣ ![]() ,﹣
,﹣ ![]() ).
).
设OE=a,则GE=2﹣a,
当CE为斜边时,则DG2=CGGE,即1=(OC﹣OG)(2﹣a),
∴1=1×(2﹣a),
∴a=1,
∴CE=2,
∴OF=OE+EF=2
∴F、P的纵坐标为﹣2,
把y=﹣2,代入抛物线的函数表达式为y=x2﹣2x﹣3得:x=1+ ![]() 或1﹣
或1﹣ ![]()
∵点P在第三象限.
∴P1(1﹣ ![]() ,﹣2),
,﹣2),
当CD为斜边时,DE⊥CE,
∴OE=2,CE=1,
∴OF=2.5,
∴P和F的纵坐标为:﹣ ![]() ,
,
把y=﹣ ![]() ,代入抛物线的函数表达式为y=x2﹣2x﹣3得:x=1﹣
,代入抛物线的函数表达式为y=x2﹣2x﹣3得:x=1﹣ ![]() ,或1+
,或1+ ![]() ,
,
∵点P在第三象限.
∴P2(1﹣ ![]() ,﹣
,﹣ ![]() ).
).
综上所述:满足条件为P1(1﹣ ![]() ,﹣2),P2(1﹣
,﹣2),P2(1﹣ ![]() ,﹣
,﹣ ![]() ).
).
【解析】已知C点的坐标,即知道OC的长,可在直角三角形BOC中根据∠BCO的正切值求出OB的长,即可得出B点的坐标.已知了△AOC和△BOC的面积比,由于两三角形的高相等,因此面积比就是AO与OB的比.由此可求出OA的长,也就求出了A点的坐标,然后根据A、B、C三点的坐标即可用待定系数法求出抛物线的解析式.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.