题目内容
17.已知$\frac{x}{2}$=$\frac{y}{3}$=$\frac{z}{4}$,则$\frac{xy+yz-2xz}{{x}^{2}+{y}^{2}+{z}^{2}}$=$\frac{2}{29}$.分析 设x=2k,y=3k,z=4k,再代入代数式进行计算即可.
解答 解:∵$\frac{x}{2}$=$\frac{y}{3}$=$\frac{z}{4}$,
∴设x=2k,y=3k,z=4k,
原式=$\frac{6{k}^{2}+12{k}^{2}-16{k}^{2}}{4{k}^{2}+9{k}^{2}+16{k}^{2}}$=$\frac{2}{29}$.
故答案为:$\frac{2}{29}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
7.某青年排球队10名队员年龄情况如下:20,20,18,19,19,19,21,21,22,22,则这10名队员年龄的众数、中位数分别是( )
| A. | 20,19 | B. | 19,19 | C. | 19,20.5 | D. | 19,20 |
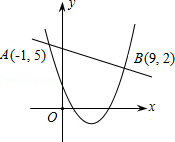 如图,一次函数y1=kx+n(k≠0)与二次函数y2=ax2+bx+c(a≠0)的图象相交于A(-1,5)、B(9,2)两点,则关于x的不等式kx+n≥ax2+bx+c的解集为-1≤x≤9.
如图,一次函数y1=kx+n(k≠0)与二次函数y2=ax2+bx+c(a≠0)的图象相交于A(-1,5)、B(9,2)两点,则关于x的不等式kx+n≥ax2+bx+c的解集为-1≤x≤9.