题目内容
16．把一个两位数的十位与个位上的数字加以交换，得到一个新的两位数，如果原来的两位数和交换后的新的两位数的差是45，试求这样的两位数中最大的是多少？分析 设原来两位数十位数字为a，个位数字为b，根据题意列出关系式，确定出最大的即可．
解答 解：设原来两位数十位数字为a，个位数字为b，
根据题意得：10a+b-（10b+a）=45，
整理得：9（a-b）=45，即a-b=5，
当a=9时，b=4，此时两位数最大，
则这样两位数中最大的是94．
点评 此题考查了有理数的大小比较，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
6．已知${（\frac{1}{2}x-k）^2}=\frac{1}{4}{x^2}+x+1$，则k的值为（ ）
| A． | ±1 | B． | ±2 | C． | -1 | D． | +1 |
如图，已知在四边形ABCD中，AB=DC，AD=BC，连接AC，BD，AC与BD交于点O，若AO=BO，AD=3，AB=2，则四边形ABCD的面积为（ ）
4．爸爸开车带着小明在公路上匀速行驶，小明每隔一段时间看到的里程碑上的数如下
9：00时看到的两位数是（ ）
| 时刻 | 9：00 | 9：45 | 12：00 |
| 碑上的数 | 是一个两位数，数字之和是9 | 十位与个位数字与9：00时所看到的正好相反 | 比9：00时看到的两位数中间多了个0 |
| A． | 54 | B． | 45 | C． | 36 | D． | 27 |
11．
如图，△ABC中，CD平分∠ACB交AB于D，DE∥BC交AC于E，若AC=9cm，DE=4cm，则AE的长度为（ ）
如图，△ABC中，CD平分∠ACB交AB于D，DE∥BC交AC于E，若AC=9cm，DE=4cm，则AE的长度为（ ）| A． | 3cm | B． | 4cm | C． | 5cm | D． | 6cm |
1．
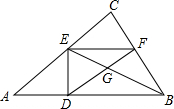如图所示，在Rt△ABC中，∠C=90°，AC=4，BC=3，AB上有一动点D以每秒4个单位的速度从点A向点B运动，当点D运动到点B时停止运动．过点D作DE⊥AB，垂足为点D，过点E作EF∥AB交BC于点F，连接BE交DF于点G，设点D运动的时间为t，当S△BDG=4S△EFG时，t的值为（ ）
如图所示，在Rt△ABC中，∠C=90°，AC=4，BC=3，AB上有一动点D以每秒4个单位的速度从点A向点B运动，当点D运动到点B时停止运动．过点D作DE⊥AB，垂足为点D，过点E作EF∥AB交BC于点F，连接BE交DF于点G，设点D运动的时间为t，当S△BDG=4S△EFG时，t的值为（ ）| A． | t=$\frac{14}{17}$ | B． | t=$\frac{12}{10}$ | C． | t=$\frac{10}{17}$ | D． | t=$\frac{8}{17}$ |
8．
如图，将三角尺ABC的一边AC沿位置固定的直尺推移得到△DEF，下列结论不一定正确的是（ ）
如图，将三角尺ABC的一边AC沿位置固定的直尺推移得到△DEF，下列结论不一定正确的是（ ）| A． | DE∥AB | B． | 四边形ABED是平行四边形 | ||
| C． | AD∥BE | D． | AD=AB |
6．已知a≥0，b≥0，且a+b=2，则（ ）
| A． | ab≤$\frac{1}{2}$ | B． | ab≥$\frac{1}{2}$ | C． | a2+b2≥2 | D． | a2+b2≤3 |