题目内容
8.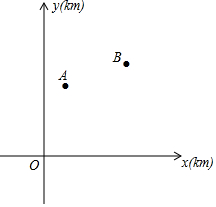 甲A、B两个村庄在坐标图纸上的坐标分别为(2,5)、(7,7),如图所示,x轴所在的位置为一条告诉公路,现要在公路上修建一个服务区P,使得服务区P到两个村庄A、B的距离之和最小.
甲A、B两个村庄在坐标图纸上的坐标分别为(2,5)、(7,7),如图所示,x轴所在的位置为一条告诉公路,现要在公路上修建一个服务区P,使得服务区P到两个村庄A、B的距离之和最小.(1)请在公路上标注出服务区P的位置;(要求尺规作图,保留必要的作图痕迹,必要时可用黑色笔加重)
(2)求出AP所在直线的解析式;
(3)为方便两村村民到服务区,拟在两个村庄到服务区之间各修建一条道路,若每修建1千米道路需费用5万元,求出所需要的总费用.
分析 (1)直接利用对称点求最短路线的方法得出P点位置;
(2)利用待定系数法求出直线AP所在直线解析式;
(3)首先构造直角三角形,再利用勾股定理得出AB′,进而得出答案.
解答  解:(1)如图所示:P点即为所求;
解:(1)如图所示:P点即为所求;
(2)B点关于x轴的对称点为:B′(7,-7),则AP所在直线即为AB′所在直线,
设过这两点的直线解析式为:y=kx+b,
可得:$\left\{\begin{array}{l}{2k+b=5}\\{7k+b=-7}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{12}{5}}\\{b=\frac{49}{5}}\end{array}\right.$,
故AP所在的直线的解析式为:y=-$\frac{12}{5}$x+$\frac{49}{5}$;
(3)所修路的长即为AB′的长,如图所示:
在Rt△AB′C中,AC=5,B′C=12,
可得:AB′=13,
故所需要的总费用为:13×5=65(万元).
点评 此题主要考查了应用设计与作图以及一次函数的应用、勾股定理等知识,正确得出P点位置是解题关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
16.某班期末考试数学的平均成绩为115分方差为768,如果每名学生都多考5分,下列说法正确的是( )
| A. | 平均分不变,方差不变 | B. | 平均分变大,方差不变 | ||
| C. | 平均分不变,方差变大 | D. | 平均分变大,方差变大 |
17.今年我市有1万名考生参加中考,为了了解这些考生的数学成绩,从中抽取500名考生的数学成绩进行统计分析,在这个问题中,下列说法:①这1万名考生的中考数学成绩的全体是总体;②每个考生是个体;③500名考生是总体的一个样本;④样本容量是500.其中说法正确的是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
18.下列调查中,适合采用全面调查(普查)方式的是( )
| A. | 对长江水质量情况的调查 | |
| B. | 对端午节期间市场上粽子质量情况的调查 | |
| C. | 对某班45名学生身高情况的调查 | |
| D. | 对某批灯泡的使用寿命的调查 |
 如图,经过原点的抛物线y=-x2+2mx(m>1)交x轴正半轴于点A,过点P(1,m)作直线PD⊥x轴于点D,交抛物线于点B,记点B关于抛物线对称轴的对称点为C,连结CB,CP.
如图,经过原点的抛物线y=-x2+2mx(m>1)交x轴正半轴于点A,过点P(1,m)作直线PD⊥x轴于点D,交抛物线于点B,记点B关于抛物线对称轴的对称点为C,连结CB,CP. 如图,在平面直角坐标系xOy中,已知直线AB:y=$\frac{2}{3}$x+4交x轴于点A,交y轴于点B.直线CD:y=-$\frac{1}{3}$x-1与直线AB相交于点M,交x轴于点C,交y轴于点D.
如图,在平面直角坐标系xOy中,已知直线AB:y=$\frac{2}{3}$x+4交x轴于点A,交y轴于点B.直线CD:y=-$\frac{1}{3}$x-1与直线AB相交于点M,交x轴于点C,交y轴于点D. 如图,在矩形ABCD中,BC>AB,∠BAD的平分线AF与BD,BC分别交于点E,F,点O是BD的中点,直线OK∥AF,交AD于点K,交BC于点G.
如图,在矩形ABCD中,BC>AB,∠BAD的平分线AF与BD,BC分别交于点E,F,点O是BD的中点,直线OK∥AF,交AD于点K,交BC于点G.