题目内容
如图,等腰Rt△ABC中,∠ACB=90°,在直角坐标系中如图摆放,点A的坐标为(0,2),点B的坐标为(6,0).(1)直接写出线段AB的中点P的坐标为______;
(2)求直线OC的解析式;
(3)动点M、N分别从O点出发,点M沿射线OC以每秒
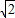 个单位长度的速度运动,点N沿线段OB以每秒1个长度的速度向终点B运动,当N点运动到B点时,M、N同时停止运动,设△PMN的面积为S(S≠0)运动时间为t秒,求S与t的函数关系式,并直接写出自变量t的取值范围.
个单位长度的速度运动,点N沿线段OB以每秒1个长度的速度向终点B运动,当N点运动到B点时,M、N同时停止运动,设△PMN的面积为S(S≠0)运动时间为t秒,求S与t的函数关系式,并直接写出自变量t的取值范围.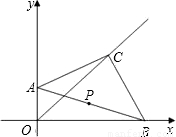
【答案】分析:(1)由于点A的坐标为(0,2),点B的坐标为(6,0),而P是线段AB的中点,由此即可确定P的坐标;
(2)如图,过点C作CE⊥OB,CD⊥OA,由此得到∠ADC=∠CEB=∠DCE=90°,接着得到∠ACD+∠ACE=90°,然后利用
等腰三角形的直线可以构造确定条件证明△ACD≌△BCE,从而得到CE=CD,进一步得到点C在第一象限的角平分线上,由此即可求出直线OC的解析式;
(3)如图,①当点M在点P左侧时,过点P作PF⊥OB,由题意可知OM=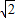 t,ON=t,然后根据已知条件可以分别把线段 MN、NF等线段用t表示,然后就可以求出函数解析式;
t,ON=t,然后根据已知条件可以分别把线段 MN、NF等线段用t表示,然后就可以求出函数解析式;
②当点M在点P右侧时,过点P作PG⊥OB,方法和①一样可以求出函数解析式解决问题.
解答:解:(1)P(3,1);
(2)过点C作CE⊥OB,CD⊥OA
∴∠ADC=∠CEB=∠DCE=90°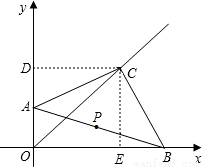 ∴∠ACD+∠ACE=90°
∴∠ACD+∠ACE=90°
在等腰Rt△ABC中
AC=BC,∠ACB=90°
∴∠BCE+∠ACE=90°(3分)
∴∠ACD=∠BCE
∴△ACD≌△BCE
∴CE=CD
∴点C在第一象限的角平分线上(4分)
∴直线OC的解析式为y=x;
(3)①当点M在点P左侧时
过点P作PF⊥OB
由题意可知
OM= tON=t(5分)
tON=t(5分)
∵点M在函数y=x上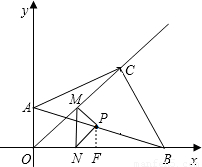
∴M(t,t)
∵N(t,0)
∴MN⊥x轴
∴MN=t
∵点P(3,1)(6分)
∴PF=1,OF=3
∴NF=OF-ON=3-t;
∴S=S梯形PMNF-S△PFN=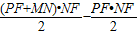 =-
=- ;
;
②当点M在点P右侧时
过点P作PG⊥OB
由①可知(8分)
∴MN⊥x轴
∴MN=t
∵点P(3,1)(9分)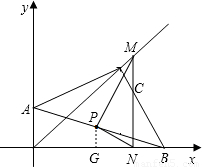
∴PG=1,OG=3
∴NG=ON-OG=t-3
∴S=S梯形PMNG-S△PGN(10分)
S=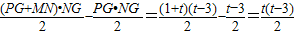
= (3<t≤6)(11分)
(3<t≤6)(11分)
综上,S=-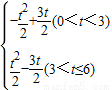 .
.
点评:此题是一次函数的综合题,首先根据中点的性质确定点的坐标,然后利用待定系数法和等腰直角三角形的性质确定函数的解析式,最后采取割补法利用面积公式解决问题.
(2)如图,过点C作CE⊥OB,CD⊥OA,由此得到∠ADC=∠CEB=∠DCE=90°,接着得到∠ACD+∠ACE=90°,然后利用
等腰三角形的直线可以构造确定条件证明△ACD≌△BCE,从而得到CE=CD,进一步得到点C在第一象限的角平分线上,由此即可求出直线OC的解析式;
(3)如图,①当点M在点P左侧时,过点P作PF⊥OB,由题意可知OM=
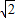 t,ON=t,然后根据已知条件可以分别把线段 MN、NF等线段用t表示,然后就可以求出函数解析式;
t,ON=t,然后根据已知条件可以分别把线段 MN、NF等线段用t表示,然后就可以求出函数解析式;②当点M在点P右侧时,过点P作PG⊥OB,方法和①一样可以求出函数解析式解决问题.
解答:解:(1)P(3,1);
(2)过点C作CE⊥OB,CD⊥OA
∴∠ADC=∠CEB=∠DCE=90°
 ∴∠ACD+∠ACE=90°
∴∠ACD+∠ACE=90°在等腰Rt△ABC中
AC=BC,∠ACB=90°
∴∠BCE+∠ACE=90°(3分)
∴∠ACD=∠BCE
∴△ACD≌△BCE
∴CE=CD
∴点C在第一象限的角平分线上(4分)
∴直线OC的解析式为y=x;
(3)①当点M在点P左侧时
过点P作PF⊥OB
由题意可知
OM=
 tON=t(5分)
tON=t(5分)∵点M在函数y=x上

∴M(t,t)
∵N(t,0)
∴MN⊥x轴
∴MN=t
∵点P(3,1)(6分)
∴PF=1,OF=3
∴NF=OF-ON=3-t;
∴S=S梯形PMNF-S△PFN=
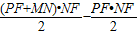 =-
=- ;
;②当点M在点P右侧时
过点P作PG⊥OB
由①可知(8分)
∴MN⊥x轴
∴MN=t
∵点P(3,1)(9分)

∴PG=1,OG=3
∴NG=ON-OG=t-3
∴S=S梯形PMNG-S△PGN(10分)
S=
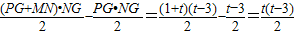
=
 (3<t≤6)(11分)
(3<t≤6)(11分)综上,S=-
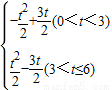 .
.点评:此题是一次函数的综合题,首先根据中点的性质确定点的坐标,然后利用待定系数法和等腰直角三角形的性质确定函数的解析式,最后采取割补法利用面积公式解决问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
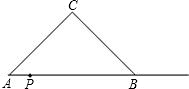 PQ=AP,以PQ为一边向上作正方形PQMN,设正方形PQMN与Rt△ABC重叠部分的面积为S.
PQ=AP,以PQ为一边向上作正方形PQMN,设正方形PQMN与Rt△ABC重叠部分的面积为S.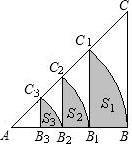 如图,等腰Rt△ABC的直角边长为4,以A为圆心,直角边AB为半径作弧BC1,交斜边AC于点C1,C1B1⊥AB于点B1,设弧BC1,C1B1,B1B围成的阴影部分的面积为S1,然后以A为圆心,AB1为半径作弧B1C2,交斜边AC于点C2,C2B2⊥AB于点B2,设弧B1C2,C2B2,B2B1围成的阴影部分的面积为S2,按此规律继续作下去,得到的阴影部分的面积S3=
如图,等腰Rt△ABC的直角边长为4,以A为圆心,直角边AB为半径作弧BC1,交斜边AC于点C1,C1B1⊥AB于点B1,设弧BC1,C1B1,B1B围成的阴影部分的面积为S1,然后以A为圆心,AB1为半径作弧B1C2,交斜边AC于点C2,C2B2⊥AB于点B2,设弧B1C2,C2B2,B2B1围成的阴影部分的面积为S2,按此规律继续作下去,得到的阴影部分的面积S3=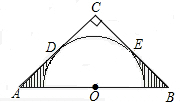 如图,等腰Rt△ABC中斜边AB=4,O是AB的中点,以O为圆心的半圆分别与两腰相切于点D、E,图中阴影部分的面积是多少?请你把它求出来.(结果用π表示)
如图,等腰Rt△ABC中斜边AB=4,O是AB的中点,以O为圆心的半圆分别与两腰相切于点D、E,图中阴影部分的面积是多少?请你把它求出来.(结果用π表示)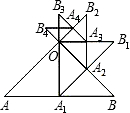 已知:如图,等腰Rt△OAB的直角边OA的长为1,以AB边上的高OA1为直角边,按逆时针方向作等腰Rt△OA1B1,A1B1与OB相交于点A2.若再以OA2为直角边按逆时针方向作等腰Rt△OA2B2,A2B2与OB1相交于点A3,按此作法进行下去,得到△OA3B3,△OA4B4,…,则△OA6B6的周长是
已知:如图,等腰Rt△OAB的直角边OA的长为1,以AB边上的高OA1为直角边,按逆时针方向作等腰Rt△OA1B1,A1B1与OB相交于点A2.若再以OA2为直角边按逆时针方向作等腰Rt△OA2B2,A2B2与OB1相交于点A3,按此作法进行下去,得到△OA3B3,△OA4B4,…,则△OA6B6的周长是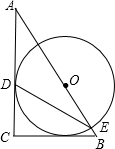 如图,等腰Rt△ABC,AC=BC,以斜边AB中点O为圆心作⊙O与AC边相切于点D,交AB于点E,连接DE.
如图,等腰Rt△ABC,AC=BC,以斜边AB中点O为圆心作⊙O与AC边相切于点D,交AB于点E,连接DE.