题目内容
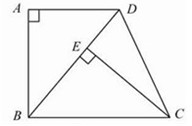
将矩形纸片ABCD，按如图所示的方式折叠，点A、点C恰好落在对角线BD
上，得到菱形BEDF.若BC=6，则AB的长为 ▲ .
上，得到菱形BEDF.若BC=6，则AB的长为 ▲ .
。翻折变换（折叠问题），折叠的性质，菱形和矩形的性质，勾股定理。
【分析】设BD与EF交于点O。
∵四边形BEDF是菱形，∴OB=OD=
BD。
∵四边形ABCD是矩形，∴∠C=90°。
设CD=x，根据折叠的性质得：OB="OD=" CD=x，即BD=2x，
在Rt△BCD中，BC2+CD2=BD2，即62+x2=（2x）2，解得：x=。
∴AB=CD=。
【分析】设BD与EF交于点O。
∵四边形BEDF是菱形，∴OB=OD=
BD。∵四边形ABCD是矩形，∴∠C=90°。
设CD=x，根据折叠的性质得：OB="OD=" CD=x，即BD=2x，
在Rt△BCD中，BC2+CD2=BD2，即62+x2=（2x）2，解得：x=
。∴AB=CD=
。
练习册系列答案
相关题目
，折叠后，点C落在AD边上的C1处，并且点B落在EC1边上的B1处．则BC的长为（ ）
s，
PAQ的面积为y cm2.（这里规定：线段是面积为0的三角形)解答下列问题：
s时，y=________cm2；
时
ABCD中，E，F分别是BC、AD上的点，且BE=DF．求证：AE=CF．
