题目内容
如图，AD⊥BC于点D，BE=AC，DE=DC，则∠ABC的度数为考点：全等三角形的判定与性质
专题：
分析：证Rt△ADC≌Rt△BDE，推出AD=BD，根据三角形内角和定理和等腰三角形性质求出即可．
解答：解：∵AD⊥BC，
∴∠ADC=∠BDE=90°，
在Rt△ADC和Rt△BDE中
∴Rt△ADC≌Rt△BDE（HL），
∴AD=BD，
∵∠BDE=90°，
∴∠ABC=∠BAD=45°，
故答案为：45°．
∴∠ADC=∠BDE=90°，
在Rt△ADC和Rt△BDE中
|
∴Rt△ADC≌Rt△BDE（HL），
∴AD=BD，
∵∠BDE=90°，
∴∠ABC=∠BAD=45°，
故答案为：45°．
点评：本题考查了全等三角形的性质和判定，等腰三角形的性质，三角形内角和定理的应用，解此题的关键是求出AD=BD．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
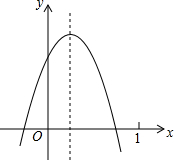已知二次函数y=ax2+bx+c（a≠0）的图象如图，则下列结论：