题目内容
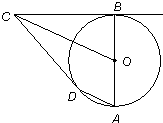21、如图，AB、CD是⊙O的直径，BC切⊙O于点B，OC平行于弦AD，求证：CD是⊙O的切线．分析：根据SAS即可证得△OCD≌△OCB，利用切线的判定定理：经过半径的外端点且与这条半径垂直的直线是圆的切线即可证得．
解答：
证明：连接OD，（1分）
∴OA=OD=OB∠OAD=∠ODA，（3分）
∵OC∥AD，
∴∠COB=∠OAD∠ODA=∠COD，
∴∠COD=∠COB，（4分）
在△OCD和△OCB中，
OB=OD，
∠COB=∠COD，
OC=OC，
∴△OCD≌△OCB，（7分）
∴∠ODC=∠OBD，（8分）
又∵BC切⊙O于点B，
∴∠ODC=∠OBD=90°，
∴CD是⊙O的切线．（10分）
证明：连接OD，（1分）∴OA=OD=OB∠OAD=∠ODA，（3分）
∵OC∥AD，
∴∠COB=∠OAD∠ODA=∠COD，
∴∠COD=∠COB，（4分）
在△OCD和△OCB中，
OB=OD，
∠COB=∠COD，
OC=OC，
∴△OCD≌△OCB，（7分）
∴∠ODC=∠OBD，（8分）
又∵BC切⊙O于点B，
∴∠ODC=∠OBD=90°，
∴CD是⊙O的切线．（10分）
点评：本题主要考查了切线的判定定理，利用判定定理可以把证切线的问题转化为正垂直的问题．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
21、如图，AB、CD是⊙O的弦，∠A=∠C．求证：AB=CD．
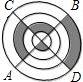如图，AB、CD是水平放置的轮盘（俯视图）上两条互相垂直的直径，一个小钢球在轮盘上自由滚动，该小钢球最终停在阴影区域的概率为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
（2013•泰安）如图，AB，CD是⊙O的两条互相垂直的直径，点O1，O2，O3，O4分别是OA、OB、OC、OD的中点，若⊙O的半径为2，则阴影部分的面积为（ ）
（2013•盘锦）如图，AB，CD是⊙O的直径，点E在AB延长线上，FE⊥AB，BE=EF=2，FE的延长线交CD延长线于点G，DG=GE=3，连接FD．
如图，AB，CD是⊙O的两条弦，且AB=CD，点M是