题目内容

如图，⊙O1、⊙O2、⊙O3、⊙O4的半径都为1，其中⊙O1与⊙O2外切，⊙O2、⊙O3、⊙O4两两精英家教网外切，并且O1、O2、O3三点在同一直线上．则：
（1）O2O4的长为
 
；
（2）若⊙O1沿图中箭头所示方向在⊙O2的圆周上滚动，到第一次与⊙O4重合的位置终止，在上述滚动过程中圆心O1移动的路径长为
 
．
分析：（1）根据两圆外切，圆心距等于两圆半径之和求解；
（2）圆心O1移动的路径是一段弧长，这段弧长的圆心是O2，半径是O1O2，旋转的度数是120度，所以根据弧长公式可得．
解答：解：（1）O2O4=1+1=2；

（2）O1移动路线是圆心角为120°半径为2的扇形弧长，
即在上述滚动过程中圆心O1移动的路径长为：
120π×2
180
=
4π
3
．
故答案为：2；
4π
3
．
点评：本题考查了相切两圆的性质和弧长的计算．解题的关键是弄准圆心角及半径和旋转的度数，然后利用弧长公式进行计算．
练习册系列答案
相关题目
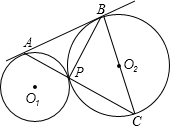精英家教网如图，⊙O1与⊙O2外切于点P，外公切线AB切⊙O1于点A，切⊙O2于点B，
（1）求证：AP⊥BP；
（2）若⊙O1与⊙O2的半径分别为r和R，求证：
AP2
BP2
=
r
R
；
（3）延长AP交⊙O2于C，连接BC，若r：R=2：3，求tan∠C的值．
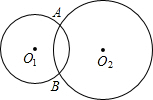精英家教网如图，⊙O1、⊙O2相交于点A、B，现给出4个命题：
（1）若AC是⊙O2的切线且交⊙O1于点C，AD是⊙O1的切线且交⊙O2于点D，则AB2=BC•BD；
（2）连接AB、O1O2，若O1A=15cm，O2A=20cm，AB=24cm，则O1O2=25cm；
（3）若CA是⊙O1的直径，DA是⊙O2的一条非直径的弦，且点D、B不重合，则C、B、D三点不在同一条直线上；
（4）若过点A作⊙O1的切线交⊙O2于点D，直线DB交⊙O1于点C，直线CA交⊙O2于点E，连接DE，则DE2=DB•DC．
则正确命题的序号是
 
．（在横线上填上所有正确命题的序号）
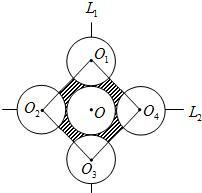精英家教网如图，⊙O1，⊙O2，⊙O3，⊙O4，⊙O的半径均为2cm，⊙O与⊙O1，⊙O3相外切，⊙O与⊙O2，⊙O4相外切，并且圆心分别位于两条互相垂直的直线L1，L2上，连接O1，O2，O3，O4得四边形O1O2O3O4，则图中阴影部分的面积为
 
cm2．（π≈3.14）
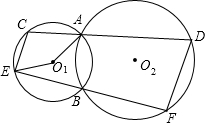精英家教网已知：如图，⊙O1和⊙O2相交于A、B两点，经过A的直线CD与⊙O1交于点C、与⊙O2交于点D，经过点B的直线EF与⊙O1交于点E、与⊙O2交于点F，连接CE、DF．若∠AO1E=100°，则∠D的度数为
 
度．
（1998•南京）如图，⊙O1和⊙O2内切于点P，⊙O2的弦AB经过⊙O1的圆心O1，交⊙O1于点C、D，若AC：CD：BD=3：4：2，则⊙O1与⊙O2的直径之比为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网