题目内容
已知Rt△ABC外接圆半径为5，直角边AC=6，则Rt△ABC内切圆半径为
2
2
．分析：利用直角三角形斜边长为外接圆直径，由勾股定理得出BC=8，再根据三角形的面积等于周长乘以半径的一半，从而得出三角形内切圆半径．
解答：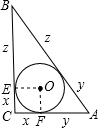
解：∵Rt△ABC外接圆半径为5，
∴Rt△ABC斜边长度为10，
∵直角边AC=6，
∴BC=
=8；
设三角形内切圆半径为r，则：
×r×（10+8+6）=
×6×8，
r=2．
故答案为：2．
解：∵Rt△ABC外接圆半径为5，∴Rt△ABC斜边长度为10，
∵直角边AC=6，
∴BC=
| 102-62 |
设三角形内切圆半径为r，则：
| 1 |
| 2 |
| 1 |
| 2 |
r=2．
故答案为：2．
点评：此题主要考查了三角形内切圆的性质以及直角三角形外接圆的性质，根据已知得出三角形三边长度是解题关键．
练习册系列答案
名校课堂系列答案
相关题目
（2011•抚顺一模）如图，已知Rt△ABC，∠ABC=90°．
，直角边AC=3，则Rt△ABC内切圆半径为________．