题目内容
10.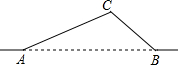 (1)如图,在△ABC中用直尺和圆规作AB边上的高CD(保留作图痕迹,不写作法).
(1)如图,在△ABC中用直尺和圆规作AB边上的高CD(保留作图痕迹,不写作法).(2)图中的实线表示从A到B需经过C点的公路,且AC=10km,∠CAB=25°,∠CBA=37°.现因城市改造需要在A、B两地之间改建一条笔直的公路.问:公路改造后比原来缩短了多少千米?(参考数据:sin25°≈0.41,cos25°≈0.91,sin37°≈0.60,tan37°≈0.75,结果精确到0.01)
分析 (1)直接利用过直线外一点作直线的垂线作法得出答案;
(2)直接利用锐角三角函数关系分别得出AD,CD,BD的长进而得出答案.
解答  解:(1)如图所示:D点即为所求;
解:(1)如图所示:D点即为所求;
(2)在Rt△ACD中,
CD=ACsin25°≈4.1(km),
AD=ACcos25°≈9.1(km),
在Rt△BCD中
BD=CD÷tan37°≈5.467(km),
AB=AD+DB=14.567km,
BC=CD÷sin37°≈6.833(km),
∴AC+BC-AB≈2.27(km),
答:公路改造后比原来缩短了2.27千米.
点评 此题主要考查了复杂作图以及锐角三角函数关系,正确应用锐角三角函数关系是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.函数y=$\sqrt{3-x}$+$\frac{1}{x-3}$中自变量x的取值范围是( )
| A. | x≤3 | B. | x<3 | C. | x≠3 | D. | x>3 |
5.如图是湖南省的行政区域平面地图,下列关于方位的说法明显错误的是( )
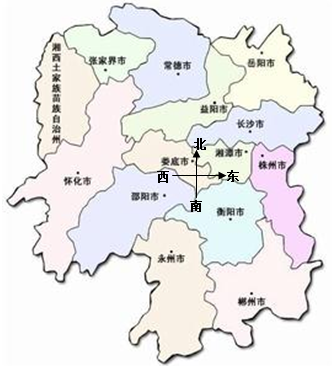

| A. | 邵阳市位于娄底市南偏西约35°的方向上 | |
| B. | 衡阳市位于永州市北偏东约60°的方向上 | |
| C. | 株洲市位于娄底市西偏北约 5°的方向上 | |
| D. | 益阳市位于长沙市北偏西约45°的方向上 |
15.下列各式中,不是二次根式的是( )
| A. | $\sqrt{-{3^2}}$ | B. | -$\sqrt{3^2}$ | C. | $\sqrt{{{(-3)}^2}}$ | D. | $\sqrt{|{-3}|}$ |
2.用尺规作图,不能作出唯一直角三角形的是( )
| A. | 已知两条直角边 | |
| B. | 已知两个锐角 | |
| C. | 已知一直角边和直角边所对的一锐角 | |
| D. | 已知斜边和一直角边 |
20.下列各式正确的是( )
| A. | $±\sqrt{0.36}$=±0.6 | B. | $\sqrt{9}=±3$ | C. | $\root{3}{(-3)^{3}}$=3 | D. | $\sqrt{(-2)^{2}}$=-2 |
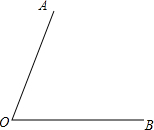 己知∠AOB=70°,根据语句画图,并填空
己知∠AOB=70°,根据语句画图,并填空