题目内容
已知：
，x2+3x为
- A.1
- B.-3和1
- C.3
- D.-1或3
A
分析：设x2+3x=y，则原方程变为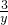
-y=2，求出方程的解，再根据根的判别式进行判断即可．
解答：设x2+3x=y，则原方程变为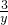：-y=2，
去分母、整理得：y2+2y-3=0，
∴（y+3）（y-1）=0，
y+3=0，y-1=0，
∴y1=-3，y2=1，
即x2+3x=-3，此方程的b2-4ac=-3＜0，
方程无解，
∴y=-3舍去，
∴x2+3x=1．
故选A，
点评：本题主要考查对解一元二次方程，用换元法解分式方程，根的判别式等知识点的理解和掌握，能综合运用这些法则进行计算是解此题的关键．
分析：设x2+3x=y，则原方程变为
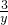-y=2，求出方程的解，再根据根的判别式进行判断即可．解答：设x2+3x=y，则原方程变为：
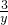-y=2，去分母、整理得：y2+2y-3=0，
∴（y+3）（y-1）=0，
y+3=0，y-1=0，
∴y1=-3，y2=1，
即x2+3x=-3，此方程的b2-4ac=-3＜0，
方程无解，
∴y=-3舍去，
∴x2+3x=1．
故选A，
点评：本题主要考查对解一元二次方程，用换元法解分式方程，根的判别式等知识点的理解和掌握，能综合运用这些法则进行计算是解此题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
，x2+3x为（ ）
，x2+3x为（ ）