题目内容
已知二次函数y=a(x-m)2-a(x-m)(a,m为常数,且a≠0).
(1)求证:不论a与m为何值,该函数的图象与x轴总有两个公共点;
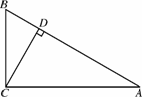
(2)设该函数的图象的顶点为C,与x轴交于A,B两点,与y轴交于点D.
①当△ABC的面积等于1时,求a的值;
②当△ABC的面积与△ABD的面积相等时,求m的值.
(1)证明:y=a(x-m)2-a(x-m)=ax2-(2am+a)x+am2+am.
当a≠0时,Δ=a2>0.
则方程ax2-(2am+a)x+am2+am=0有两个不相等的实数根.
所以,不论a与m为何值,该函数的图象与x轴总有两个公共点.
(2)解:① y=a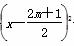 -
-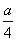 ,
,
所以点C的坐标为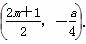 .
.
当y=0时,a(x-m)2-a(x-m)=0.
解得x1=m,x2=m+1.所以AB=1.
当△ABC的面积等于1时,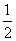 ×1×
×1×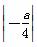 =1.
=1.
所以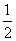 ×1×
×1×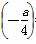 =1,或
=1,或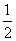 ×1×
×1×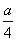 =1.
=1.
所以a=-8,或a=8.
②当x=0时,y=am2+am,
所以点D的坐标为(0, am2+am).
当△ABC的面积与△ABD的面积相等时,
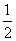 ×1×
×1×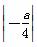 =
=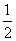 ×1×| am2+am |.
×1×| am2+am |.
所以m=-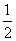 ,或m=
,或m=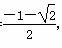 ,或m=
,或m=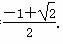 .
.

练习册系列答案
相关题目
根据下列表格中的对应值,判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的根的个数是( )
A.0 B.1 C.2 D.1或2
| x | 6.17 | 6.18 | 6.19 | 6.20 |
| y=ax2+bx+c | 0.02 | -0.01 | 0.02 | 0.04 |

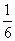 B.
B.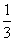 C.
C.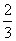
 的值为________.
的值为________.

 ,规定
,规定 ,若
,若 ,则
,则 的值为 。
的值为 。