Question

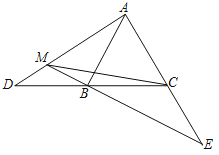
【题目】如图，在等边△ABC中，AB＝4，D、E分别为射线CB、AC上的两动点，且BD＝CE，直线AD和BE相交于M点，则CM的最大值为（　　）

A.2B.C.3D.4

Answer 1

【答案】D

【解析】

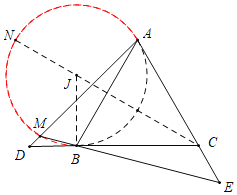
首先证明∠AMB＝60°，推出点M的运动轨迹是图中红线（在△ABM的外接圆⊙J上），连接CJ，延长CJ交⊙J 于N，当点M与N重合时，CM的值最大．

如图，

∵△ABC是等边三角形，

∴BA＝CB，∠ABC＝∠ACB＝60°，

∴∠ABD＝∠BCE＝120°，

∵BD＝CE，

∴△ABD≌△BCE（SAS），

∴∠D＝∠E，

∵∠DBM＝∠EBC，

∴∠DMB＝∠BCE＝120°，

∴∠AMB＝60°，

∴点M的运动轨迹是图中红线（在△ABM的外接圆⊙J上），

连接CJ，延长CJ交⊙J 于N，当点M与N重合时，CM的值最大，

在Rt△JCB中，BJ＝BCtan30＝，JC＝2BJ＝，

∴CN＝+＝4，

∴CM的最大值为4，

故选：D．