题目内容
解下列不等式、不等式组,并将其解集在数轴上表示出来:
①
-1<
②
.
①
| x+5 |
| 2 |
| 3x+2 |
| 2 |
②
|
考点:解一元一次不等式组,在数轴上表示不等式的解集,解一元一次不等式
专题:
分析:(1)首先两边同时乘以6,去分母,再移项、合并同类项即可;
(2)分别计算出两个不等式的解集,再根据大小小大中间找可确定不等式组的解集.
(2)分别计算出两个不等式的解集,再根据大小小大中间找可确定不等式组的解集.
解答:解:(1)去分母得:x+5-2<3x+2,
移项得:x-3x<2+2-5,
合并同类项得:-2x<-1,
把x的系数化为1得:x>
,
在数轴上表示:
 ;
;
(2)
,
由①得:x>-6,
由②得:x<6,
不等式组的解集为:-6<x<6,
在数轴上表示:
 .
.
移项得:x-3x<2+2-5,
合并同类项得:-2x<-1,
把x的系数化为1得:x>
| 1 |
| 2 |
在数轴上表示:
 ;
;(2)
|
由①得:x>-6,
由②得:x<6,
不等式组的解集为:-6<x<6,
在数轴上表示:
 .
.点评:此题主要考查了解一元一次不等式(组),关键是掌握解不等式的步骤:①去分母;②去括号;③移项;④合并同类项;⑤化系数为1.

练习册系列答案
相关题目
下列四个算式中,有一个算式与其他三个算式的计算结果不同,则该算式是( )
| A、2-3 |
| B、-12 |
| C、(-1)3 |
| D、(-1)2 |
下列函数中,y是x的一次函数的是( )
A、y=
| ||
| B、y=-5x2 | ||
C、y=
| ||
D、y=2
|
将二次函数y=(x-1)2-3的图象沿x轴翻折,所得图象的函数表达式为( )
| A、y=-(x-1)2+3 |
| B、y=(x+1)2-3 |
| C、y=-(x+1)2-3 |
| D、y=(x-1)2+3 |
已知抛物线y=(m-1)x2+4x-3(m为常数)与x轴有两个交点,则m的取值范围是( )
A、m>-
| ||
B、m<-
| ||
C、m≥-
| ||
D、m>-
|
某种商品原价是100元,经过两次提价后的价格是120元,求平均每次提价的百分率.设平均每次提价的百分率为x,下列所列方程中正确的是( )
| A、100(1+x)2=120 |
| B、100(1-x)2=120 |
| C、120(1+x)2=100 |
| D、120(1-x)2=100 |
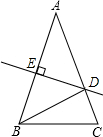 如图,在△ABC中,AB=AC,AB的中垂线DE交AC于点D,交AB于E点,如果BC=10,△BDC的周长为22,那么△ABC的周长是( )
如图,在△ABC中,AB=AC,AB的中垂线DE交AC于点D,交AB于E点,如果BC=10,△BDC的周长为22,那么△ABC的周长是( )