题目内容
4.在数学活动课上,老师提出了一个问题,希望同学们进行探究.在平面直角坐标系中,若一次函数y=kx+6的图象与x轴交于点A,与y轴交于点B,与反比例函数y=$\frac{6}{x}$的图象交于C、D两点,则AD和BC有怎样的数量关系?
同学们通过合作讨论,逐渐完成了对问题的探究.
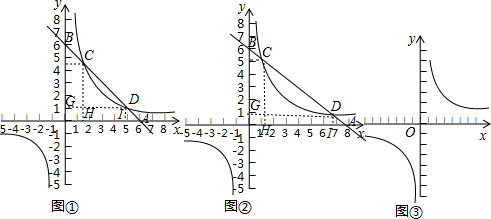
小勇说:我们可以从特殊入手,取D进行研究(如图①),此时我发现AD=BC.
小攀说:在图①中,分别从点C、D两点向两条坐标轴作垂线,根据所学知识可以知道有两个图形的面积是相等的,并能求出确定的值,而且在图②中,此时S矩形FCHO=S矩形GDIO,这一结论仍然成立,即四边形OHCF的面积=四边形OIDG的面积,此面积的值为6.
小高说:我还发现,在图①或图②中连接某两个已知点,得到的线段与AD和BC都相等,这条线段是GH.
(1)请完成以上填空;
(2)请结合以上三位同学的讨论,对图②所示的情况下,证明AD=BC;
小峰突然提出一个问题:通过刚才的证明,我们可以知道当直线与双曲线的两个交点都在第一象限时,AD=BC总是成立的,但我发现当k的取值不同时,这两个交点有可能在不同象限,结论还成立吗?
(3)请你结合小峰提出的问题,在图③中画出示意图,并判断结论是否成立.若成立,请写出证明过程;若不成立,请说明理由.
分析 (1)根据题目的叙述即可直接解答;
(2)连接GH,GC,DH,证明S△CGH=S△GHD.则CD∥GH,然后根据平行四边形的性质求解;
(3)与(2)解法相同,证明S△CGH=S△GHD.则点C,D到GH的距离相等,然后利用平行四边形的性质证得.
解答 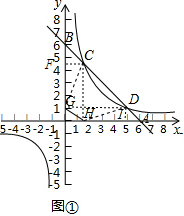 解:(1)S矩形FCHO=S矩形GDIO,这一结论仍然成立,即的四边形OHCF面积=四边形OIDG的面积,此面积的值为6.
解:(1)S矩形FCHO=S矩形GDIO,这一结论仍然成立,即的四边形OHCF面积=四边形OIDG的面积,此面积的值为6.
在图①或图②中连接某两个已知点,得到的线段与AD和BC都相等,这条线段是GH.
故答案是:四边形OHCF,四边形OIDG,6,GH;
(2)成立,证明如下:
如图①,连接GH,GC,DH,
∵点C,D是反比例图象上的点,
∴S矩形FCHO=S矩形GDIO.
∴$\frac{1}{2}{S_{矩形FCHO}}=\frac{1}{2}{S_{矩形GDIO}}$.
∴S△CGH=S△GHD.
∴点C,D到GH的距离相等.
∴CD∥GH.
∴四边形BCHG和四边形GHAD都是平行四边形.
∴BC=GH,GH=DA.
即AD=BC;
(3)画出图形,得到GH,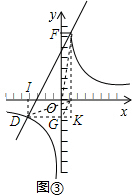
∵点C,D是反比例图象上的点,
∴S矩形FCHO=S矩形GDIO.
∴$\frac{1}{2}{S_{矩形FCHO}}=\frac{1}{2}{S_{矩形GDIO}}$.
∴S△CGH=S△GHD.
∴点C,D到GH的距离相等.
∴CD∥GH.
∴四边形BCHG和四边形GHAD都是平行四边形.
∴BC=GH,GH=DA.
即AD=BC.
点评 本题考查了反比例函数的性质以及反比例函数比例系数k的几何意义,注意题目之间的联系是解决本题的关键.

练习册系列答案
相关题目
19.今年我区吉安镇柑桔喜获丰收,根据柑桔季节性及以往销售经验,销售时间不超过12周,每千克售价y(元)与销售时间x(周)之间的关系如下表:
(1)请你从所学过的一次函数和二次函数中确定哪种函数关系能表达y与x的变化规律(不需说明理由),并写出y关于x的函数关系式.
(2)根据销售经验,第1周每千克售价30元时,当周可以销售1200千克水果;以后售价每降低2元,当周销售量可以增加400千克,通过计算估计最多第几周的销售金额就可以达到60800元.
(3)设第9周的销售量仍满足(2)中的关系,根据销售经验,从第9周后,每周的销售量均比前一周下降900千克,而售价与时间仍满足(1)中的关系,柑桔通过前9周的销售后,只剩5000千克.现准备将这批柑桔全部批发给某水果商,那么每千克的批发价至少为多少元时,才能获得不低于依销售经验按周销售的金额?
(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{5}$≈2.24,$\sqrt{6}$≈2.45,$\sqrt{7}$≈2.65)
| 销售时间x(周) | 1 | 2 | 3 | 4 | 5 | 6 | … |
| 每千克售价y(元) | 30 | 28 | 26 | 24 | 22 | 20 | … |
(2)根据销售经验,第1周每千克售价30元时,当周可以销售1200千克水果;以后售价每降低2元,当周销售量可以增加400千克,通过计算估计最多第几周的销售金额就可以达到60800元.
(3)设第9周的销售量仍满足(2)中的关系,根据销售经验,从第9周后,每周的销售量均比前一周下降900千克,而售价与时间仍满足(1)中的关系,柑桔通过前9周的销售后,只剩5000千克.现准备将这批柑桔全部批发给某水果商,那么每千克的批发价至少为多少元时,才能获得不低于依销售经验按周销售的金额?
(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{5}$≈2.24,$\sqrt{6}$≈2.45,$\sqrt{7}$≈2.65)
9. 体能抽测小组从某市6000名九年级男生中,随机抽取了500名进行50米跑测试,并根据测试结果绘制了如下尚不完整的统计图表.解答下列问题:
体能抽测小组从某市6000名九年级男生中,随机抽取了500名进行50米跑测试,并根据测试结果绘制了如下尚不完整的统计图表.解答下列问题:
(1)a=125,b=250;
(2)补全条形统计图;
(3)试估计这6000名九年级男生中50米跑到良好和优秀等级的总人数.
 体能抽测小组从某市6000名九年级男生中,随机抽取了500名进行50米跑测试,并根据测试结果绘制了如下尚不完整的统计图表.解答下列问题:
体能抽测小组从某市6000名九年级男生中,随机抽取了500名进行50米跑测试,并根据测试结果绘制了如下尚不完整的统计图表.解答下列问题:| 等级 | 人数/名 |
| 优秀 | a |
| 良好 | b |
| 及格 | 100 |
| 不及格 | 25 |
(2)补全条形统计图;
(3)试估计这6000名九年级男生中50米跑到良好和优秀等级的总人数.
11. 已知,如图,C、D是OA上两点,E、F是OB上两点,下列各式中,表示∠AOB错误的是( )
已知,如图,C、D是OA上两点,E、F是OB上两点,下列各式中,表示∠AOB错误的是( )
 已知,如图,C、D是OA上两点,E、F是OB上两点,下列各式中,表示∠AOB错误的是( )
已知,如图,C、D是OA上两点,E、F是OB上两点,下列各式中,表示∠AOB错误的是( )| A. | ∠COE | B. | ∠AOF | C. | ∠DOB | D. | ∠EOF |
 如图,是一个正方体纸盒展开图,按虚线折成正方体后,若使相对面上的两数互为相反数,则A、B、C表示的数依次是-5,-π,$\frac{3}{2}$.
如图,是一个正方体纸盒展开图,按虚线折成正方体后,若使相对面上的两数互为相反数,则A、B、C表示的数依次是-5,-π,$\frac{3}{2}$. 如图,AB=8,AD=AC=4,AE=2,∠BAD=∠CAE,AM⊥BC,AN⊥DE,则AM:AN=2.
如图,AB=8,AD=AC=4,AE=2,∠BAD=∠CAE,AM⊥BC,AN⊥DE,则AM:AN=2. 在△ABC中,AB=6,BC=8,CA=7,延长CA至点P,使∠PBA=∠C,求AP的长.
在△ABC中,AB=6,BC=8,CA=7,延长CA至点P,使∠PBA=∠C,求AP的长.